Znajdź równanie płaszczyzny zawierającą punkt P(2,1,1) oraz prostą l : {𝑥+𝑦−𝑧 Andrzej : Znajdź równanie płaszczyzny zawierającą punkt P(2,1,1) oraz prostą l : {𝑥+𝑦−𝑧=0 𝑥−𝑦+2𝑧−4=0.Obliczyłem iloczyn wektorowy z wektorów kierunkowych płaszczyzn z równania krawędziowego co dalej proszę pomóc.

jc: Każdą płaszczyznę zawierającą rozważaną prostą można zapisać w postaci a(x+y−z)+b(x−y+2z−4)=0, (a,b)≠(0,0) Dobieramy a,b tak, aby punkt (2,1,1) leżał na płaszczyźnie. a(x+y−z)+b(x−y+2z−4)=0 2a−b=0, a=1, b=2 Wynik: 3x−y+3z−8=0

Andrzej : Jak się nazywa ta postać w której zapisałeś płaszczyznę?

Andrzej : Ewentualnie jak zapisać równanie prostej?

Jerzy: Masz już policzony wektor kierunkowy prostej.Teraz wybierz dowolny punkt A na tej prostej. Iloczyn wektorowy wektora AP i obliczonego wektora, to wektor normalny szukanej płaszczyzny.

Jerzy: I nie używaj pojęcia „wektor kierunkowy płaszczyzny”, tylko „wektor normalny”.

Andrzej : Dobra mam wektor kierunkowy prostej i chcę obliczyć dowolny punkt A tylko jaki wzór ma ta prosta ? w sensie jakie mam X0 Y0 Z0 na tej prostej?

Jerzy: Musisz znaleźć równanie parametrycze prostej będącej krawędzią przecięcia podanych płaszczyzn

Andrzej : Dobra zadanie było proste bardziej niż myślałem ,po prostu warto sobie strzelić kawe czasem.Dzięki.

jc: Jerzy, licząc dwa kolejne iloczyny wektorowe zwiększamy ryzyko pomyłki, oraz tracimy czas, który może się przydać na rozwiązanie pozostałych zadań. A zadanie rozwiązuje się niemal w pamięci (cały rachunek powyżej).

Jerzy: Zgoda,ale najwyraźniej studenci nie znają wzoru, z którego skorzystałeś.

Andrzej : No nie znam tego wzoru i nie przypominam sobie z wykładu ale może to kwestia okrojenia materiału na studiach niestacjonarnych albo za mało czasu by wszystko zrealizować.

jc: Pewnie nie było. Mało kto o tym mówi, szczególnie jak jest mało czasu. Uzasadnienie jest proste. Zastanów się dlaczego płaszczyzna a(x+y−z)+b(x−y+2z−4)=0 zawiera prostą część wspólną płaszczyzn x+y−z=0, x−y+2z−4=0. Może lepiej nie ryzykować? Nie wiadomo, czy jak to zostanie ocenione, choć na mnie nieznane mi sposoby rozwiązania robią zwykle pozytywne wrażenie .

Jerzy: Ale nie zawsze na oceniającym.

6latek: Pytanie Jesli plaszczyzna przechodzi przez punkt to oznacza ze ten punkt nalezy do tej plaszczyzny?

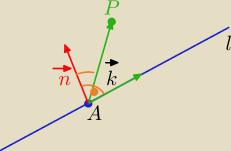
Mila: II sposób ( więcej liczenia) P(2,1,1) l : 𝑥+𝑦−𝑧=0, 𝑥−𝑦+2𝑧−4=0 równanie krawędziowe prostej Przekształcam na równanie parametryczne x=t− parametr, t∊R t+y−z=0 t−y+2z−4=0 ====== + z+2t−4=0 z=4−2t t+y−(4−2t)=0 y=4−3t ========= l: x=t y=4−3t z=4−2t , t∊R Patrz rysunek: A=(0,4,4)∊l l⊂π, P=(2,1,1)∊π k^→[1,−3,−2] wektor kierunkowy prostej AP^→[2,−3,−3] n^→=[1,−3,−2] x [2,−3,−3]= [3,−1,3] wektor normalny płaszczyzny π: 3*(x−2)−(y−1)+3*(z−1)=0⇔ π: 3x−y+3z−8=0 równanie płaszczyzny w postaci ogólnej ============== Wynik jak u JC

6latek: Dzien dobry Milu Mozesz odpowiedziec na moje pytanie ?

Jerzy: Cześć małolat . Tak.

6latek: Witaj Jerzy dziekuje za odpowiedz .

Mila: Tak. ( 16:04)

Jerzy: Witaj Milu Mam wrażenie ,że autor postu właśnie tak rozwiązał to zadanie.

Mila: Witajcie Panowie W takim razie niepotrzebnie pisałam Nie doczytałam, że rozwiązał.

6latek: P=(2,1,1) x+y−z=0 x−y+2z−4=0 x+y−z+ λ(x−y+2z−4)=0 2+1−1+λ(2−1+2−4)=0 2−λ=0 λ=2 x+y−z+2(x−y+2z−4)=0 x+y−z+2x−2y+4z−8=0 3x−y+3z−8=0 rownanie tej plaszczyzny