Zbior wartości funkcji Emilia: Nie przekształcając wzoru funkcji y = −(x−4)(x+2) podaj jej monotoniczność, oraz zbiór wartości.

Eta:

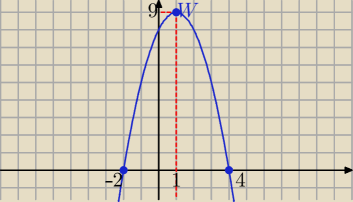
	4−2
xw=p=		=1 yw=f(1)= ...=9
	2

W(1,9) i a=−1<0 parabola "łapami" do dołu ZW= (−∞, 9> f(x)↗ ⇔ x∊( −∞, 1) f(x)↘ ⇔ x∊(1,∞)

Mila: 1) Parabola skierowana w dół. 2) Miejsca zerowe: x₁=4 lu x₂=−2 3) Współrzędne wierzchołka paraboli:

	4+(−2)
xw=		=1 (x=1 − oś symetrii paraboli)
	2

y_w=f(1)=−(1−4)*(1+2)=9 4) Monotoniczność : f(x) ↑ dla x∊(−∞,1> f(x)↓ dla x∊<1,∞) 5) Zw_f=(−∞,9>

Eta: W zadaniu nie jest napisane : wskaż "maksymalne" przedziały

Emilia: właśnie nie czaje skąd wzieliście wierzchołek

ABC: wierzchołek jest położony symetrycznie pomiędzy miejscami zerowymi

Jerzy: Odcięta wierzchołka jest środkiem odcinka (x₁,x₂)