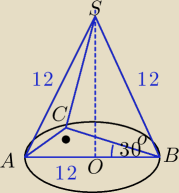
POMOCY !?!?! Kimici: Witam, ktoś miałby ochotę mi może wytłumaczyć jak rozwiązać takie zadanie ? Wszystkie krawędzie boczne ostrosłupa mają taką samą długość. Podstawą tego ostrosłupa jest trójkąt prostokątny, którego jeden z kątów jest równy 30°, a przeciwprostokątna ma długość 12. Największa ściana boczna ostrosłupa jest trójkątem równobocznym. A) Wykaż, że jedna z krawędzi podstawy ma długość równą wysokości ostrosłupa. B) Oblicz pole powierzchni całkowitej ostrosłupa.

iteRacj@: Skorzystaj z tego, że jeżeli wszystkie krawędzie boczne ostrosłupa mają taką samą długość, to na podstawie ostrosłupa można opisać okrąg, a spodek wysokości ostrosłupa to środek tego okręgu. W tym zadaniu trójkąt prostokątny, który jest podstawą tego ostrosłupa, ma przeciwprostokątną o długości 12, więc taką długość mają krawędzie boczne tego ostrosłupa. A/ Skorzystaj z podobieństwa ΔABC i ΔOSB. B/ Pole powierzchni całkowitej ostrosłupa obliczysz, dzięki temu, że znasz długości wszystkich krawędzi.