ekstrema lokalne a dziedzina funkcji i pochodnej funkcji kasiaba: Czy żeby istniało ekstremum lokalne w punkcie, to musi ten punkt należeć do dziedziny pochodnej funkcji i dziedziny funkcji czy nie?

ABC: do dziedziny funkcji tak, do dziedziny pochodnej nie

kasiaba: a mogłabym prosić o szersze wyjaśnienie?

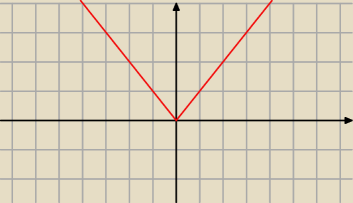
ABC: najprostszy przykład chyba bezwzględna wartość , dla x=0 jest minimum lokalne a nawet globalne, a pochodna w tym punkcie nie istnieje (pochodne jednostronne są różne: −1 i 1)

kasiaba: a jakie będą ekstrema dla funkcji f(x) = x + 3ln(x) ?

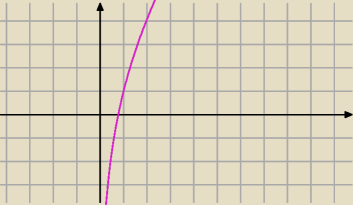
ABC: dziedzina tej funkcji to (0,+∞) i pochodna tej funkcji

	3
f'(x)=1+		jest dodatnia w całej dziedzinie, więc funkcja rośnie od −∞ do +∞ i nie
	x

posiada żadnego ekstremum

kasiaba: Dziękuję

kasiaba: A co, gdy dojdzie wartość bezwzględna? f(x) = x + 3ln(|x|)

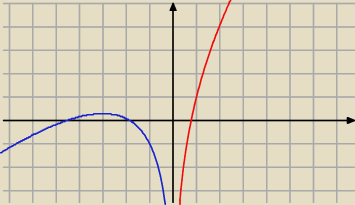
ABC: wtedy się sytuacja zmieni

	3
albowiem dla x<0 funkcja x+ln(−x) znów ma pochodną 1+		ale teraz dla x=−3 ta pochodna
	x

się zeruje i zmienia znak w otoczeniu tego punktu

ABC: