ostrosłup mar: Kąt między krawędzią boczną a podstawą ostrosłupa prawidłowego czworokątnego ma miarę α, a kąt między jego krawędziami bocznymi β. a) Wykaż, że cosβ = sin²α b) Oblicz V, jeżeli β=60stopni, a krawędź boczna 4. Po pierwsze nie jestem pewien, czy kąt między krawędziami bocznymi to na pewno ten zaznaczony na zielono.

	16
Jeśli tak to V =		√10
	3

Ale nie wiem jak rozwiązać pkt (a).

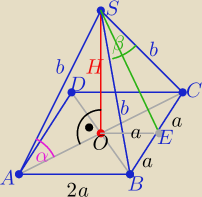Eta: |AO|=a√2

	a√2		2a2
W ΔAOS sinα=		⇒ sin2α=
	b		b2

z tw. cosinusów w ΔBCS

	b2+b2−4a2		2a2
cosβ=		⇒ cosβ= 1−
	2*b*b		b2

⇒ cosβ= 1−sin²α ⇒ cosβ= cos²α ============== c.n.w. b) dla β=60^o trójkąt BCS równoboczny to h_b= a√3 i 2a=4 h_b= 2√3 W Δ OES H=√(2√3)²−2²=√12−4=2√2

	1
V=		*16*2√2
	3

	32√2
V=
	3

===========

Eta: Poprawiam chochliki (sorry) Miało być:

	a√2		2a2
cosα=		⇒ cos2α=
	b		b2

....................

	2a2
cosβ= 1−
	b2

cosβ=1−cos²α ⇒ cosβ= sin²α =============