zad
zad: całka podwójna ∫∫(4x−2y)dxdy
trójkąt A(1,1) B(3,3) C(−1,3)
| ⎧ | −1≤x≤3 | |
| ⎩ | 2≤y≤−x |  
|
Nie mam pojęcia
7 lut 00:47
jc: Strasznie abstrakcyjne ujęcie. Co oznacza A(1,1)?
7 lut 00:58
zad:
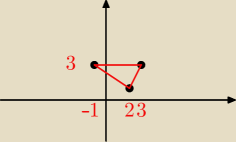
7 lut 01:05
Adamm:
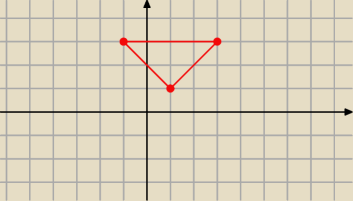
−y+2≤x≤y
1≤y≤3
7 lut 01:08
jc: Parametryzajacja
s,t → (x,y)=P + s(Q−P) + t(R−P), s,t ≥0, s+t ≤ 1
Podstawiasz i liczysz.
Inna parametryzacja.
s,t → (1−s)P+ s ((1−t)Q + tR)
0≤s≤1, 0≤t≤1
Pamiętaj o jakobianie!
7 lut 01:12
jc: Jak tak, jak u Adamma, to
możemy przyjąć
1 ≤ y ≤ 3
2−y ≤ x ≤ y
czyli ∫13 dy ∫2−yy f(x,y) dx
7 lut 01:22
zad: Tylko skąd te obszary są
1 ≤ y ≤ 3
2−y ≤ x ≤ y

Nie rozumiem tego
7 lut 01:25
jc: Z rysunku Adamma.
7 lut 01:27
Mila:
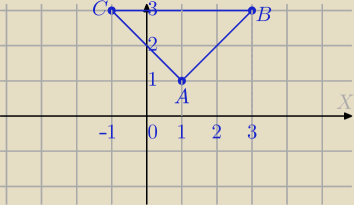
∫∫(4x−2y)dxdy
D: A(1,1) B(3,3) C(−1,3)
Prosta AC:
y=ax+b,
3=−a+b
1=a+b ⇔
2b=4, b=2 i 1=a+2
a=−1
AC: y=−x+2
Prosta AB:
y=x
==========
∫∫
D(4x−2y)dxdy=
x=−1∫
1[
y=−x+2∫
y=3(4x−2y) dy ]dx+
+
x=1∫
3[
y=x∫
y=3(4x−2y) dy ]dx=
7 lut 17:57
Mila:
Względem OY będzie jedna całka.
7 lut 17:58



 −y+2≤x≤y
1≤y≤3
−y+2≤x≤y
1≤y≤3
 Nie rozumiem tego
Nie rozumiem tego
 ∫∫(4x−2y)dxdy
D: A(1,1) B(3,3) C(−1,3)
Prosta AC:
y=ax+b,
3=−a+b
1=a+b ⇔
2b=4, b=2 i 1=a+2
a=−1
AC: y=−x+2
Prosta AB:
y=x
==========
∫∫D(4x−2y)dxdy=x=−1∫1[y=−x+2∫y=3(4x−2y) dy ]dx+
+x=1∫3[y=x∫y=3(4x−2y) dy ]dx=
∫∫(4x−2y)dxdy
D: A(1,1) B(3,3) C(−1,3)
Prosta AC:
y=ax+b,
3=−a+b
1=a+b ⇔
2b=4, b=2 i 1=a+2
a=−1
AC: y=−x+2
Prosta AB:
y=x
==========
∫∫D(4x−2y)dxdy=x=−1∫1[y=−x+2∫y=3(4x−2y) dy ]dx+
+x=1∫3[y=x∫y=3(4x−2y) dy ]dx=