Znajdź równanie płaszczyzny do ktorej należy punkt P=(1,2,1) oraz prosta l:x-1/ Ziołek: Znajdź równanie płaszczyzny do ktorej należy punkt P=(1,2,1) oraz prosta l: (x−1)/1=y/2+(z+1)/1.Nie wiem czy dobrze to rozwiązałem.Zrobiłem tak na prostej l wyznaczyłem dwa punkty Q=(4,6,2) S=(2,2,0) pierwsze pytanie czy te punkty należą do tej prostej zrobiłem to tak ,żeby równanie powstawianiu x y z się zgadzało.Później utworzyłem wektory PQ i PS i zrobiłem iloczyn wektorowy PQXPS=(−4,4,−4).I stworzyłem równanie płąszczyzny: −4(x−1)+4(y−2)−4(z−1)=0 i teraz kolejne pytanie czy x0 y0 z0 w równaniu płaszczyzny mogą być wspołrzedne punktu P(1,2,1) po skróceniu równania otrzymałem −x+y−z=0.

Mila: P=(1,2,1) l:

x−1		y		z+1
	=		=		takie równanie prostej?
1		2		1

Ziołek: tak

jc: x−1=y/2=z+1 Wolę rozwiązanie z pękiem płaszczyzn. 2x−y−2=0 2z−y+2=0 a(2x−y−2)+b(2z−y+2)=0 P=(1,2,1) −2a+2b=0 a=b=1/2 x−y+z=0 Dobrze masz

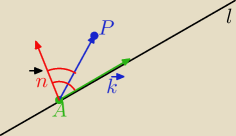
Mila: P=(1,2,1) Punkt A=(1,0,−1) ∊l k^→=[1,2,1] − wektor kierunkowy prostej AP^→[0,2,2] n^→=[0,2,2] x [1,2,1]=[−2,2,−2] wektor normalny płaszczyzny −2*(x−1)+2*(y−0)−2*(z+1)=0 −2x+2+2y−2x−2=0 /:(−2) π: x−y+z=0 albo tak: [−2,2,−2] || [1,−1,1] − wektor normalny płaszczyzny P∊π x−1−1*(y−2)+z−1=0 x−1−y+2+z−1=0 x−y+z=0 i masz to samo równanie =========

Ziołek: Mila Punkt A musi być koniecznie (1,0,−1) czy może być np(2,2,1)?

jc: (1,0,−1) jest najłatwiejszy do odczytania.

Ziołek: okej okej czyli po prostu punkt A był wyznaczony z równania prostej.Dzięki wszystko jasne.

Mila: Nie musi być A, ale musi to być punkt należący do prostej l. (2,2,1) nie należy do prostej l (2,2, 0) może być Napisz równanie płaszczyzny z (2,2,0)

Ziołek: −2(x−2)+2(y−2)−2(z−0)=−2x+4+2y−4−2z=−2x+2y−2z=−x+y−z

Mila: Nie możesz tak zapisywać : 23:39, tylko tak: −2(x−2)+2(y−2)−2(z−0)=0 −2x+4+2y−4−2z=0 −2x+2y−2z=0 /:(−2) x−y+z=0 Dobranoc