zespolone, moduły, narysować MMK: Bardzo proszę o pomoc z tym. Korzystając z interpretacji geometrycznej modułu różnicy liczb zespolonych wyznaczyć i narysować zbiory liczb zespolonych spełniających warunki |z + 3i| < |z − 1 − 4| I bardzo ładnie proszę nie linkować tych dwóch postów w których to zadanie nie zostało rozwiązane.

PW: Popraw prawą stronę.

MMK: |z + 3i| < |z − 1 − 4i|

PW: |z−u| to długość odcinka między z a u (odległość od z do u). Tutaj odległośc od z do (−3i) ma być mniejsza niż odległość od z do (1+4i). Inaczej mówiąc punkt z ma być bliżej (−3i) niż (1+4i). Dla punktów z leżących na symetralnej odcinka o końcach (−3i), (1+4i) odległości te są równe. A dla jakich punktów spełniona jest zadana nierówność?

MMK: Środek odcinka będzie w punkcie (1/2, 1/2) ? A równanie symetralnej y=1/7x +6/14 ? I wtedy rozwiązaniem będzie wszystko powyżej symetralnej ?

PW: A = (0, −3). B = (1, 4)

	1		1
S = (		,		)
	2		2

AB^→[1, 7], a więc symetralna ma równanie x+7y+C = 0 po podstawieniu wsp. S

	1		7
		+		+C=0
	2		2

C = −4, symetralna x+7y−4=0. Rozwiązania − poniżej symetralnej (mają być bliżej (0, −3)).

MMK: Robiąc zwykłaym sposobem na symetralna wychodzi mi za każdym razem y=1/7x +6/14 .

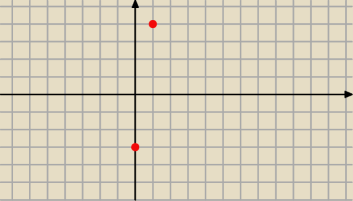
PW: Często mylę się w rachunkach, ale symetralna tego odcinka jest nachylona do osi OX pod takim kątem α, że tgα < 0,

	1
tgα≠
	7

MMK: Wydaje mi się że po prostu zgubiłam minus w którymś miejscu. Dzięki za pomoc.