| 1 | ||
miarę α. Wykaż, że cosinus kata między sąsiednimi ścianami bocznymi jest równy − | ||
| tg2α |
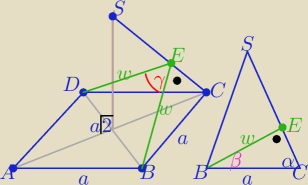|DB|=a√2 , |DB|2=2a2
Z tw. cosinusów w ΔBDE
| w2+w2−2a2 | a2 | |||
cosγ= | ⇒ cosγ=1− | 2 | ||
| 2w*w | w |
| w | w2 | 1 | a2 | |||||
i w ΔBCE sinα= | ⇒ sin2α= | to | = | |||||
| a | a2 | sin2α | w2 |
| 1 | 1−sin2 | cos2α | 1 | |||||
cosγ= 1− | = − | = − | = −ctg2α= − | |||||
| sin2α | sin2α | sin2α | tg2α |
| 1 | ||
cosγ= − | , kąt γ −−− rozwarty | |
| tg2α |