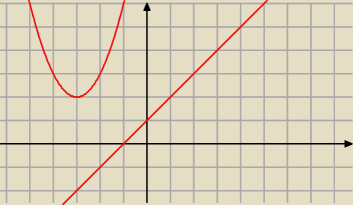
zadanie maturalne, rozszerzenie WSiP 2019 iteRacj@: Pewnie nie wszyscy pisali ostatnie próbne rozszerzenie, a zadania były ciekawe. Może ktoś będzie mieć chęć rozwiązać. Zadanie za 6 punktów, to może Maciess podejdzie ambitnie? Dana jest parabola o równaniu y = x² + 6x +11 oraz prosta o równaniu y = x +1. Rozważamy wszystkie odcinki AB takie, że punkt A leży na danej paraboli, a punkt B leży na danej prostej. Oblicz długość najkrótszego z odcinków AB oraz dla tego najkrótszego odcinka współrzędne jego końca D leżącego na paraboli.

Adamm: odległość (x, y) od prostej to

|y−x−1|
√2

innymi słowy mamy zminimalizować |x²+5x+10| = x²+5x+10 mimum mamy dla x = −5/2, równe 15/4