Optymalizacja
pheri: Zadanie: Rozważmy zbiór wszystkich prostokątów wpisanych w kwadrat o boku a tak, że boki
tych prostokątów są parami równoległe do przekątnych danego kwadratu. Oblicz długości boków
tego prostokąta, który ma największe pole.
Jak się zabrać za to zadanie?
6 lut 16:35
iteRacj@:
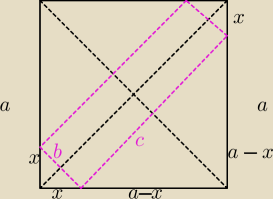P=b*c
1/ długości boków b,c wyznacz z tw. Pitagorasa dla trójkątów prostokątnych o bokach b,x,x oraz
c,a−x,a−x
2/ otrzymasz wzór na P(x), poszukaj maksimum tej funkcji
6 lut 16:56
Adamm:
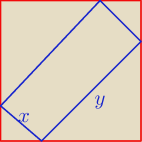√2a−x = y, x∊[0,
√2a]
P(x) = (
√2a−x)x
maksimum ma dla x =
√2a/2
P(
√2a/2) = a/2
6 lut 16:59
pheri: Prowadzę te obliczenia i wychodzi mi tak:
b=x√2
c=√2(a−x)
Czy zatem P(x) nie będzie równe: P(x)=bc=x√2*√2(a−x)=−2x2+2ax?
Czy coś źle policzyłem? Mógłbym prosić o pomoc?
6 lut 17:39
iteRacj@:
Sposób podany przez Adamma jest najkrótszy i daje odpowiedź prawie bez obliczeń.
W moim sposobie jest więcej liczenia. Zwróć uwagę, że obu rysunkach, co innego zostało
oznaczone przez x.
6 lut 18:02
iteRacj@:
Jesli liczysz podanym przez mnie sposobem, zacznij od założenia 0<x<a.
P(x) policzyłeś dobrze. Masz funkcję kwadratową, znajdź jej minimum, sóorzystając ze
wspołrzędnych wierzchołka.
6 lut 18:05
pheri: | | −B | | a | |
Już wszystko jasne: P(x)=−2x2+2ax, zatem x= |
| = |
| |
| | 2A | | 2 | |
| | a√2 | | a | | a√2 | |
b=x√2= |
| oraz c=√2(a− |
| )= |
| |
| | 2 | | 2 | | 2 | |
Zatem: b=c, co oznacza, że figura wpisana w kwadrat o podstawie a to kwadrat.
6 lut 18:06
pheri: Mam rację?
6 lut 18:06
iteRacj@: *korzystając ze współrzędnych wierzchołka
6 lut 18:06
iteRacj@: tak jest
6 lut 18:07
pheri: No i super, dziękuję za wyjaśnienie zadania!
6 lut 18:08
pheri: W gwoli wyjaśnienia, poprawki − ''w kwadrat o BOKU a''*
6 lut 18:13