Oblicz pole powierzchni całkowitej bryły. Dzik: Mógłby ktoś pomóc mi z tym zadaniem ? Podstawą ostrosłupa jest trapez prostokątny o dłuższej podstawie 8 i kącie ostrym 45°. Spodkiem wysokości ostrosłupa jest środek okręgu wpisanego w podstawę, a wysokość ostrosłupa jest równa promieniowi tego okręgu.Oblicz pole powierzchni całkowitej bryły.

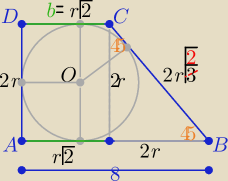
Eta: Podstawą trapez jak na rys. 1 ( pomyłkowo wpisałam √3 oczywiście ma być 2r√2 wierzchołkiem ostrosłupa S i spodkiem O −− środek okręgu wpisanego w trapez z warunku okręgu wpisanego w ten trapez mamy a+b=2r+2r√2 to a=2r+r√2=8 ⇒ r=4(2−√2 = H ostrosłupa to r²=32(3−2√2) ponieważ w podstawę można wpisać okrąg to wszystkie ściany boczne ostrosłupa są nachylone pod tym samym kątem α i z treści zadania r=H więc α=45^o −− kąt nachylenia wszystkich ścian bocznych do podstawy więc wszystkie wysokości ścian bocznych h_b=r√2 P_p = (8+r√2*r= r²√2+8r

	1
P(ADS)=		*r√2*2r = r2√2
	2

	1
P(ABS)=		*r√2*8 = 4r√2
	2

	1
P(BCS)=		*r√2*2r√2= 2r2
	2

	1
P(DCS)=		*r√2*r√2= r2
	2

po zsumowaniu: P_c=(3+2√2)r²+4(2+√2)r i po podstawieniu za r i za r² P_c=32(3−2√2)(3+2√2) +4(2+√2)4(2−√2)=32+16*2 P_c= 64 j² =========

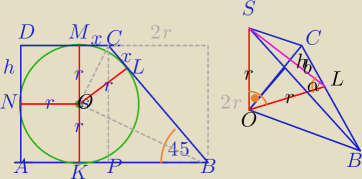Mila: 1)|AB|=8 |KB|=|BL|=8−r − punkty styczności okręgu są jednakowo odległe od wierzchołków kąta |PB|=2r −ΔCPB− Δprostokątny równoramienny |BC|=2r*√2 x=2r√2−8+r 2) |AB|=r+2r√2−8+r+2r 4r+2r√2−8=8 4r+2r√2=16 /:2 2r+r√2=8 r*(2+√2)=8 /*(2−√2) r*(4−2)=8(2−√2) r=4*(2−√2) 3)|AB|+|DC|=|AD|+|BC| z warunku wpisania okręgu w czworokąt⇔ |AB|+|DC|=2r+2r√2=2r*(1+√2) Obw_ABCD=2*2r(1+√2)=4r*(1+√2) 4)

	4r*(1+√2)
PABCD=		*r=2r2*(1+√2)
	2

5)

	1
Pb=		*ObwABCD*hb
	2

H=r z treści ściany boczne są nachylone pod tym samym kątem do płaszczyzny podstawy. W ΔSOL: h_b=r√2 P_b=2r(1+√2)*r√2=2r²√2*(1+√2) P_c=2r²*(1+√2)+2r²√2*(1+√2)= =2r²*(1+√2)*(1+√2)= =2r²*(3+2√2) P_c=2*(4*(2−√2))²*(3+2√2)=64 ================ Sprawdzaj rachunki

Eta:

Mila: