 P 45: Dwie płaszczyzny H1: x=y, H2: y+z=0 przecinają się wzdłuż prostej odległej od punktu
(1,0,0) o … (obliczyć).
A więc. mam dwie płaszczyzny
H1: x−y=0 n=[1,−1,0]
H2: y+z=0 n=[0,1,1]
mnożę wektorowo − wyszło mi v=[−1,−1,1]
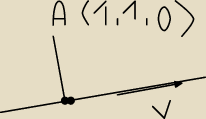
dalej narysowałem sobie takie coś
<rysunek>
Jak obliczyć punkt zaznaczony kropką? Dobrze w ogóle to robię?
Proszę o pomoc
P 45: Dwie płaszczyzny H1: x=y, H2: y+z=0 przecinają się wzdłuż prostej odległej od punktu
(1,0,0) o … (obliczyć).
A więc. mam dwie płaszczyzny
H1: x−y=0 n=[1,−1,0]
H2: y+z=0 n=[0,1,1]
mnożę wektorowo − wyszło mi v=[−1,−1,1]
dalej narysowałem sobie takie coś
<rysunek>
Jak obliczyć punkt zaznaczony kropką? Dobrze w ogóle to robię?
Proszę o pomoc 
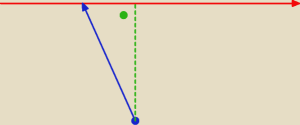 [1, 0, 0] to ten niebieski punkt, koniec wektora to jakiś wybrany punkt [x, x, −x]
chodzi o to by niebieski wektor, to jest, [x, x, −x]−[1, 0, 0], był
prostopadły to czerwonej prostej
jak tak będzie, to długość tego wektora to będzie odpowiedź
czyli wektor kierunkowy czerwonej prostej musi być prostopadły do [x, x, −x]−[1, 0, 0]
a to wiemy jak wyrazić za pomocą iloczynu skalarnego
dalej już prosto
[1, 0, 0] to ten niebieski punkt, koniec wektora to jakiś wybrany punkt [x, x, −x]
chodzi o to by niebieski wektor, to jest, [x, x, −x]−[1, 0, 0], był
prostopadły to czerwonej prostej
jak tak będzie, to długość tego wektora to będzie odpowiedź
czyli wektor kierunkowy czerwonej prostej musi być prostopadły do [x, x, −x]−[1, 0, 0]
a to wiemy jak wyrazić za pomocą iloczynu skalarnego
dalej już prosto
| 2 | ||
t=− | ||
| 3 |
| 2 | 2 | 2 | ||||
P=( | , | ,− | ) | |||
| 3 | 3 | 3 |
| √6 | ||
|AP|=√(2/3−1)2+(2/3−1)2+(−2/3)2=√6/9=√2/3= | ||
| 3 |
| √6 | ||
|AP|= | ||
| 3 |