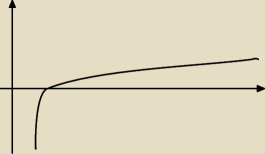
dlaczego ? Aleks: jak to jest wykres pochodnej funkcji f(x)=xlnx, czyli f'(x)=lnx+1, to może mi ktoś wyjaśnić z jakiej racji funkcja ma być malejąca w przedziale x należy (o, ¹_e) Mam wyznaczyć przedziały monotoniczności i ekstrema lokalne i moim zdaniem funkcja tylko rośnie więc nie ma ekstremów lokalnych, ale jak pisałam na forum to było, że funkcja przechodzi z malejącą w rosnącą, więc ma tam ekstremum, tyle, że ja tego nie widzę. HELP!

Jerzy: Mylisz kolego wykres funkcji z wykresem pochodnej Z tego wykresu wynika,że pochodna zmienia znak w punkcie x = 1/e i tam ma minimum lokalne.

Jerzy: Sorry .... koleżnko , nie zauważyłem

Aleks: czyli funkcja maleje w x ∊ (0, ¹_e) i rośnie w x ∊(¹_e, +∞) i ma ekstremum lokalne w punkcie (¹_e, f(¹_e)) ?

Aleks: minimum lokalne

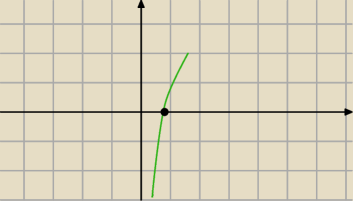
Jerzy: To jest orientacyjny wykres pochodnej, a czarny punkt to x = 1/e i jak widzisz tam pochodna zmienia znak z ujemnego na dodatni, czyli funkcj ma minimum lokalne.

Jerzy: Dokładnie tak.

Aleks: ok, dziękuję