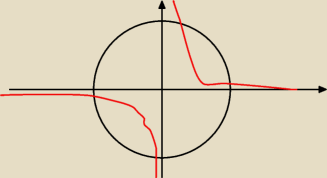
pole pod wykresem Trębacz: Pole pod wykresem x²+y² = 3 i y=√2/x; tak więc wyliczyłem, że wykresy przecinają się w punkatch x∊{−1,1,√2,−√2} czyli pole to będzie 2* całka na przedziale od 1 do √2 ∫√3−x² − ^√2_x dx tylko pytanie jak się za tą całkę zabrać. Próbowałem przez części − u = √3−x², du = −^x_√3−x² ale to doprowadziło mnie do całki tej postaci: https://www.wolframalpha.com/input/?i=integral+of+x%5E2+%2F+(3-x%5E2)%5E(1%2F2) a tutaj to już przez postawienie ani części nie da się bardziej ruszyć. Proszę o pomoc

wredulus_pospolitus: w wolframie koło wyniku całki masz taki przycisk 'step by step solution'. Nawet jeżeli nie wykupiłeś dostępu to będziesz miał 'sam początek' rozwiązania. Zauważysz jak sprytnie tutaj tą całkę można było rozwiązać

Trębacz: oooo dziękuję bardzo! Teraz to ma sens