Interpolacja Langrange'a

Interpolacja Langrange'a student: Dla badanej funkcji f(x) = |x| w przedziale <−1,1>, punkty interpolacyjne: [−1, −0.5, 0, 0.5, 1] dokonaj interpolacji wielomianowej Lagrange'a ze sprawdzeniem. Jak będzie wyglądała tabelka poniżej? i Xi fi

4 lut 20:44

ABC:

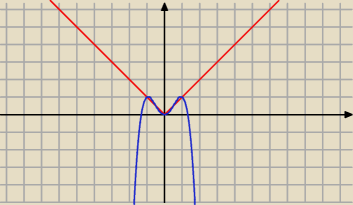
powinno ci wyjść

	4		7
−		x⁴+		x²
	3		3

4 lut 21:00

student: Dobrze rozpisuję? i Xi fi 0 −1 1 −0,5 2 0 3 0,5 4 1

4 lut 21:07

ABC: punkty (−1,1) (−0.5,0.5) (0,0) (0.5,0.5) (1,1)

4 lut 21:10

student:

	(x−(−¹₂))(x−0)(x−¹₂)(x−1)
Czyli dla L0 =
	(−1−(¹₂))(−1−0)(−1−¹₂)(−1−1)

4 lut 21:16

ABC: ja to policzyłem w sposób uproszczony odgadując postać wielomianu z uwagi na symetrię , ale jak ci wykładowca każe z tych wzorów to rób

4 lut 21:43

student: Tylko czy dobrze zapisałem?

4 lut 21:50

Mariusz: Kiedyś napisałem programik do interpolacji wielomianowej Uwzględniłem w nim metodę polegającą na rozwiązaniu układu równań, interpolację Lagrange , oraz interpolację Newtona jednak kod mam na innym dysku

4 lut 21:56

ABC: rozumiem że mianownik pierwszy nawias masz (−1+0.5) , jeśli tak to ok

4 lut 21:57

student: Jak będzie wyglądała kolumna fi? Resztę obliczeń powinienem sobie poradzić.

4 lut 22:13

ABC: z tego co widzę musisz jeszcze 3 wielomiany policzyć takie jak ten który napisałeś i potem ich kombinację

4 lut 22:16

ABC: następny jakoś tak

(x+1)(x−0)(x−0.5)(x−1)

(−0.5+1)(−0.5−0)(−0.5−0.5)(−0.5−1)

4 lut 22:20

student: Tak, wiem. Mam na brudno policzone. Potem trzeba podstawić do funkcji interpolującej W = f0 * L0 + f1 * L1 + f2* L2 + f3 * L3 + f4 * L4?

4 lut 22:21

ABC: L₀(x)+0.5L₁(x)+0.5L₃(x)+L₄(x)

4 lut 22:23

student: OK, dziękuję za pomoc. Dobrej nocy życzę.

4 lut 22:26

ABC:

4 lut 22:28