. sylwiaczek: ile rozwiazan rownania sinxIcosxI=1/4 nalezy do przedzialu <0, 172π>? robie to na 2 przypadki cosx≥0 i cosx<0

	3		5
czyli sin2x= 1/2 dla xe <0+2kπ, π/2+2kπ> U <		π +2kπ,		π+ 2kπ>
	2		2

	3
i sin2x= −1/2 dla xe (π/2 +2kπ,		π+2kπ)
	2

i z tego wychodzi mi 688 rozwiazan, a w odp jest 344, gdzie robie zle?

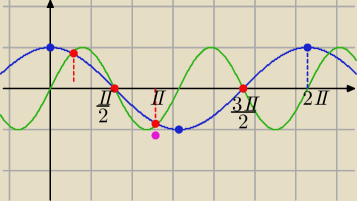Eta: Rozpatrz przedział <0,2π> y= cosx≥0 dla x∊<0, π/2> U <3π/2, 2π> y= sin(2x) w tych przedziałach są 4 rozwiązania ( "czerwone kropki" y= cosx<0 dla x∊(π/2,3π/2) jest jedno rozwiązanie fioletowa kropka −− pokrywa się z czerwoną z poprzedniego przedziału zatem w przedziale <0,172π> mamy (172:2)*4= 344 rozwiązań ============================