Ciągłość i różniczkowalnosc Łukasz: Sprawdzić, w jakich punktach jest ciągła, a w jakich różniczkowalna funkcja określona wzorem

	⎧	x2 gdy x należy do wymiernych
f(x)=	⎨
	⎩	x4 w przeciwnym wypadku

POMOCY!

Adamm: ciągła może być tylko tam gdzie x² = x⁴, to jest, x = 0 lub x = 1 lub x = −1 można łatwo sprawdzić że lim_x→1 f(x) = lim_x→−1 f(x) = 1 oraz lim_x→0 f(x) = 0 (x²)' = 2x, (x⁴)' = 4x³ idąc do ±1 po wymiernych, mamy ±2, a po niewymiernych, ±4 więc nie jest różniczkowalna w punktach ±1 za to w 0 już jest

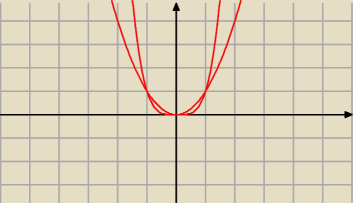
Adamm: A tak ta funkcja wygląda

Łukasz: Dzięki!