.
Adamm:
Jaka jest definicja prostej w bardziej abstrakcyjnych przestrzeniach?
4 lut 17:16
Adamm:
Chodzi o to, wiadomo jak definiować proste w R2 itp.
Czym byłaby prosta w ogólniejszej przestrzeni.
4 lut 17:19
jc: W przestrzeniach afinicznych to jasne (t→P+tv).
W przestrzeniach, gdzie można nadać sens dłuości linii, to najkrótsza linia
(np, koło wielkie na sferze). Pewnie są jeszcze jakieś inne podejścia.
4 lut 17:37
jc: W przestrzeni rzutowej to też trochę coś innego, ale czy tak bardzo?
4 lut 17:38
Adamm:
Bo chodzi o coś takiego.
Przy aksjomatach Euklidesa mamy takie pojęcia jak 'punkt' czy 'prosta'
Czytałem te definicje, ale nadal nie wiem co to tak naprawdę jest
Wydaje mi się że definicje te są po prostu przegadane, tak żeby
wydawało się że coś tak naprawdę znaczą, a nie znaczą nic.
Może zadam inne pytanie.
Nie ustalajmy co to jest prosta, ani co to jest punkt.
Jakie muszą być między nimi relacje?
4 lut 18:06
PW:
Nie znaczą nic, bo to są pojęcia pierwotne. Aksjomaty opisują relacje między tymi pojęciami
pierwotnymi.
Przykład:
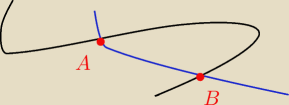
Przez każde dwa różne punkty przechodzi dokładnie jedna prosta.
Ten aksjomat objaśnia: wyobrażaj sobie prostą jak chcesz i rysuj jak chcesz, ale nie może być
tak jak na rysunku wyżej (te dwa twory nie są prostymi).
4 lut 18:51
 Nie znaczą nic, bo to są pojęcia pierwotne. Aksjomaty opisują relacje między tymi pojęciami
pierwotnymi.
Przykład:
Przez każde dwa różne punkty przechodzi dokładnie jedna prosta.
Ten aksjomat objaśnia: wyobrażaj sobie prostą jak chcesz i rysuj jak chcesz, ale nie może być
tak jak na rysunku wyżej (te dwa twory nie są prostymi).
Nie znaczą nic, bo to są pojęcia pierwotne. Aksjomaty opisują relacje między tymi pojęciami
pierwotnymi.
Przykład:
Przez każde dwa różne punkty przechodzi dokładnie jedna prosta.
Ten aksjomat objaśnia: wyobrażaj sobie prostą jak chcesz i rysuj jak chcesz, ale nie może być
tak jak na rysunku wyżej (te dwa twory nie są prostymi).