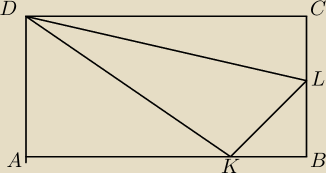
W prostokącie ABCD punkt K leży na boku AB (...) wykaż, że..... Julka: W prostokącie ABCD punkt K leży na boku AB w taki sposób, że |AK|=2|KB|, a punkt L jest środkiem boku BC (rysunek). Wiedząc, że |AD|= x i |CD|= y, wykaż, że P△_DKL = ¹₃P▭_ABC_

fwckn:

Julka: Zauważyłam, że na końcu zjadło "D", więc od razu poprawię: P△_DKL = ¹₃P▭_ABCD

ICSP: |AD| = x |CD| = y

	2
|AK| =		x
	3

	1
|KB| =		x
	3

	1
|BL| = |LC| =		y
	2

P_ΔKLD = P_▭ABCD − P_ΔAKD − P_ΔKLB − P_ΔDCL =

	1		2		1		1		1		1		1
= xy −		*		x y −		x *		*		y − x *		*		y =
	2		3		3		2		2		2		2

	1		1		1		12 − 4 − 1 − 3		1
= xy[ 1 −		−		−		] = xy [		] =		xy =
	3		12		4		12		3

1
	P▭ABCD
3

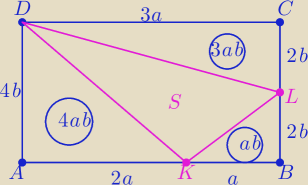Eta: P(ABCD)=P= 12ab S= 12ab−(4ab+ab+3ab)= 4ab

	4ab		1
to P(KLD)= S=		=
	12ab		3

	1
S=		P
	3

Julka: Dziękuję za pomoc! już wszystko rozumiem : )