. sylwiaczek: wsrod prostokatow ktorych dwa wierzcholki naleza do paraboli o rownaniu y=(x+3)² zas dwa pozostale do prostej k: y=4 znajduje sie taki ktorego pole jest najwieksze. oblicz wspolrzedne wierzcholkow tego prostokata i jego pole wiem ze jest to zadanie na forum, ale nic stamtad nie rozumiem, ktos pomoze?

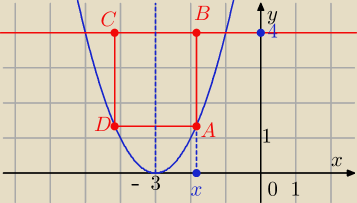
Janek191: p = − 3 q = 0 A = ( x , ( x + 3)²) B = (x , 4) P = 2*(x + 3)*( 4 − ( x + 3)²) = ( 2 x + 6)*( 4 − x² − 6 x − 9) = = 8 x − 2 x³ −12 x² − 18 x + 24 −6 x² − 36 x −54 = = −2 x³ − 18 x² − 46 x − 30 f(x) = − 2 x³ − 18 x² − 46 x − 30 f '(x) = − 6 x² − 36 x − 46 = 0 ⇔ 3 x² + 18 x + 23 = 0 Δ = 324 − 276 = 48 = 16*3 √Δ = 4√3

	− 18 + 4√3		2
x =		= − 3 +		√3
	6		3

	2		4
A = ( − 3 +		√3,		)
	3		3

	2
B = ( − 3 +		√3 , 4)
	3

	2
C = ( − 3 −		√3, 4)
	3

	2		4
D = ( −3 −		√3 ,		)
	3		3

Jak się nie pomyliłem

M: P = 2*(x + 3)*( 4 − ( x + 3)²) Skąd się to wzięło? Rozumiem, że liczymy pole, ale skąd?

janek191: I AD I = 2*( x − (−3)) = 2*( x + 3) I AB I = ( y_B − y_A) = ( 4 − (x + 3)²)