relacja Jędruś: W zbiorze wszystkich kół na płaszczyźnie dana jest relacja : A∼B ⇐⇒ koła A,B maja˛ten sam środek. Sprawdzić, że jest to relacja równoważności i wyznaczyć wszystkie jej klasy abstrakcji. Pomoże ktoś?

iteRacj@: Sprawdź, czy relacja jest: zwrotna → czy każde koło ma środek w tym samym punkcie co ono samo? symetryczna → jeśli koło pierwsze ma ten sam środek co koło drugie, to czy to drugie ma środek tam, gdzie to pierwsze? przechodnia → koło pierwsze ma środek tam gdzie koło drugie, drugie tam gdzie trzecie, czy pierwsze i trzecie mają środki w tym samym punkcie?

Jędruś: To już wiem, ale za bardzo nie czaję tych klas abstrakcji...

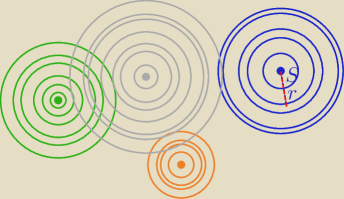
iteRacj@: Do klasy abstrakcji wyznaczonej przez koło k(S,r) należą wszystkie koła o środku S i dowolnym promieniu (ponieważ warunek podany w zadaniu dotyczy tylko środka koła). Teraz pozostaje tylko zastanowić, ile punktów płaszczyzny może być środkami okręgów ← tyle właśnie jest klas abstrakcji tej relacji.

iteRacj@: *środkami kół