Zrobiłam kilka zadań i prosiłabym o sprawdzenie, czy poprawnie. nauqa: Zrobiłam kilka zadań i prosiłabym o sprawdzenie, czy poprawnie. Zad.1 Rozwiąż każdą z nierówności:

	x		1
1)x2+√(x2)≤2 ; 2)		>0 ; 3) (x−		)(x2+2x+4)≥0
	2−x		8

Zakoduj trzy pierwsze cyfry po przecinku rozwinięcia dziesiętnego najmniejszej liczby, która spełnia jednocześnie te trzy nierówności.

	x		1
1)x2+|x|−2≤0 2)		>0 3) (x−		)(x2+2x+4)≥0
	2−x		8

Δ=1²−4*1*(−2) x(2−x)>0 x²x+4≥0 −>Δ<0 x∊R

	1
Δ=9 √Δ=3 x∊(0;2) x−		≥0
	8

	−1−3		1
x1=		=−2 x≥
	2		8

	−1+3
x2=		=1
	2

x∊<−2;1>

	1
czyli x∊<		;1>
	8

Zad.2

	1		1		x2−2
Rozwiąż nierówność		+		≥		i oblicz sumę liczb naturalnych
	x		x+1		x(x+1)

spełniających tę nierówność

x+1+x		x2−2
	≥
x(x+1)		x(x+1)

2x+1		x2−2
	−		≥0
x(x+1)		x(x+1)

−x2+2x+3
	≥0
x(x+1)

−(x−3)(x+1)x(x+1)≥0 Liczby naturalne spełniające tę nierówność to x∊<1;3>, czyli 1,2,3. Ich suma 1+2+3=6

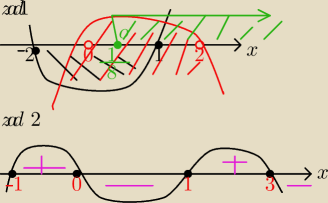
iteRacj@: zad.2 Okresl dziedzinę wyrażenia wymiernego i uwzględnij, rysując. Liczba 1 nie jest miejscem zerowym ostatniego wielomianu, a u Ciebie na rysunku została zaznaczona.

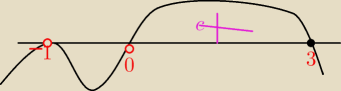
nauqa: D: x∊R/{−1,0} czyli rozwiązanie tej nierówności to x∊(0;3> Teraz już dobrze?

iteRacj@: Tak, zgadza się.

iteRacj@: zad.2/ 1/ x∊R, x²+|x|−2≤0 to przekształcenie wyjsciowej nierówności jest poprawne, ale dalej błąd. Powinnaś skorzystać z własności wartości bezwzględnej x²=|x|² i rozwiązać nierówność |x|²+|x|−2≤0 . Jest to nierówność kwadratowa, zmienną jest |x|, możesz podstawic znienną pomocniczą t, t≥0. Twoja nierówność z 10:27 nie jest kwadratowa. 2/,3/ dobrze