Cześć, czy mógłby ktoś rzucić okiem, czy dobrze zrobiłem to zadanie?
W liczbach zespolonych (w postaci trygonometrycznej) rozwiązać równanie z3 − i√3 = −1.
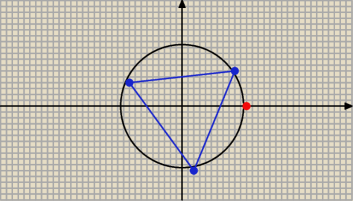
Otrzymane rozwiązania przedstawić na płaszczyźnie zespolonej.
z3= −1+ i√3
z=3√−1+i√3
|z|=√(−1)2+3=2
| 1 | ||
cosφ=− | ||
| 2 |
| √3 | ||
sinφ= | ||
| 2 |
| 2π | 2π | |||
z=2(cos | +isin | ) | ||
| 3 | 3 |
| 2π | 2π | |||
z0=3√2(cos | +isin | ) | ||
| 9 | 9 |
| 8π | 8π | |||
z1=3√2(cos | +isin | ) | ||
| 9 | 9 |
| 14π | 14π | |||
z2=3√2(cos | +isin | ) | ||
| 9 | 9 |
| 5^2 | 52 |
| 2^{10} | 210 |
| a_2 | a2 |
| a_{25} | a25 |
| p{2} | √2 |
| p{81} | √81 |
| Kliknij po więcej przykładów | |
|---|---|
| Twój nick | |