rozwiąż nierówność marcin: x⁴+2x³+x²/x−1+6x²<0 mnoze przez dol to daje mi x⁴+2x³+x²<0 wyciagam przed nawias x² −> x²(x²+2x+1)<0 x²<0 a z nawiasu licze delte wychodzi x0 jeden pierwiastek x0=−1 nie wiem co dalej zrobic jak to oznaczyc na osi... Moze ktos rzuci okiem na to

Jerzy: Katastrofa. Na jakiej podstawie mnożysz przez mianownik ?

marcin: to cos mi sie ladnie pomylilo...

marcin: Jak zaczac rozwiazywac takie zadanie?

wredulus_pospolitus: 1) zapis −−− TRAGEDIA Czy wy naprawdę nie wiecie do czego służą nawiasy Ani nie zdajecie sobie sprawy z czegoś takiego jak kolejność wykonywania działań 2) 'mnożę przez dół' −− dlaczego? Dlaczego tak? 3) x² < 0 "WAAAAT"

Jerzy: Nie wolno, bo nie znasz znaku mianownika. .... ⇔ x²*(x² + 2x +1)*(6x² + x −1) < 0 ⇔ x²(x + 1)²*(6x² +x − 1) < 0 Teraz ostatni trójmian rozłóż na czynniki.

marcin: Dlaczego mnoze przez mianownik?

Jerzy: Przecież sam to napisałeś.

marcin: Kurcze bo jak pomnoze przez mianownik to z lewej strony znika a po prawej jest 0 wiec i tak wyjdzie 0

Jerzy: Do ciężkiej cholery, napisałem ci wyraźnie ,że nie wolno pomnożyć obustronnie przez mianownik, bo on przyjmuje zarówno wartośi dodatnie i ujemne !

Jerzy: Patrz 12:02 ... i tak to rozwiązuj.

marcin: x=0, x=−1, x=1/3, x=−1/2 Tylko kurde jakos nie moge sobie zobrazować jak doszlo do tego ze mianownik zaczelismy mnozyc przez gore

marcin:

x4+2x3+x2
	<0
x−1+6x2

Jerzy:

a
	< 0 ⇔ a*b < 0
b

Złe miejsca zerowe. To nie jest równanie, tylko nierówność

marcin:

	a
czyli jak bede widzial takie zadanko to moge smialo korzystac z tego		<0 = a*b<0
	b

Jerzy: Sorry... miejsca zerowe są dobre.

marcin: czyli wrzucam dol na gore i rozbijam na pare pierwiastków

Jerzy: Nie "równa się", tylko "jest równoważne".

Jerzy: Rozwiąż coś takiego:

x − 2
	> 0
x −1

wredulus_pospolitus: Zacznijmy od tego, że możesz zauważyć, ze licznik jest ≥0 Więc powyższa nierówność (z pierwszego postu) będzie spełniona jedynie gdy mianownik < 0

Jerzy: To co napisał wredulus widać dokładnie 12:02 x²*(x+ 1)² > 0

marcin: zrobilem przyklad od Jerzego

x−2
	>0
x−1

(x−2)(x−1)>0 x=2 x=1

Jerzy: Na razie tylko wyznaczyleś miejsca zerowe lewej strony, a masz rozwiazć nierwówność ! To nie jest równanie ! Musisz wyznaczyć przedziały, do jakich należy x !

marcin: Dobra widze ze licznk jest ≥0 to mianownik musi byc ujemny zeby bylo <0 ale nie widze co dalej skoro widze ze mianownik jest ≥0 a dol ujemny

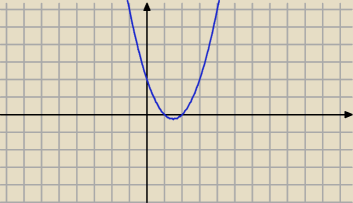
Jerzy: Tutaj masz wykres lewej strony nierówności ( trójmianu kwadratowego). Kiedy przyjmuje wartości dodatnie ?

Jerzy: Co ty ku...bredzisz ? Co to jest u ciebie "dół " ? Masz do rozwiąznia nierówność: 6x² + x − 1 < 0 i po zadaniu !

marcin: jak jest mniejsza od zera to nie powinny byc ramiona w dol?

marcin: (−∞,−1/3)u(−1/2,∞)

Jerzy: Ten rysunek 12:27 dotyczy przykładu 12:19

marcin: Dobra topornie idzie przez moje braki ale wracajac do zadania

x4+2x3+x2
	<0 rozumiem ze licznik olewam i licze po prostu pierwiastki z
x−1+6x2

mianownika?

wredulus_pospolitus: ale licznik 'możesz olać' dopiero jak napiszesz dlaczego go olewasz

marcin: jak zadam pytanie dlaczego mozna "odpuscic" to pewnie padniecie bo pewnie jest to wyzej napisane..

marcin: chwila chyba rozumiem

Jerzy: No to teraz ustal, kiedy mianownik jest ujemny .

marcin:

	a
jak widze ze gora jest ≥0 to zeby spelnilo sie rownanie		<0 to MIANOWNIK musi byc ujemny
	b

czyli licze ten ujemny mianownik

marcin: w sensie pierwiastki mianownika i zapisuje ich przedzial i to tyle ?

Jerzy: Kur.. nie wytrzymam. Co to jest "góra" ? Co to znaczy liczę ujemny mianownik ? Masz ustalić dala jakich wartości x mianownik przyjmuje wartości ujemne !

marcin: nie wiem czemu nazwalem to ujemnym mianownikiem ale chodzilo ze licze przedzial dla x

Jerzy: Odpowiedz na proste pytanie: Dla jakich wartości x , trójmian kwadratowy: 6x² + x −1 < 0 ?

marcin: √Δ =5 x= 1/3 , −1/2 zaznaczam to na osi i wychodzi przedzial (−∞,−1/2)u(1/3,∞)

marcin: nie no zle musialem zaznaczyc przedzial bo to sensu nie ma

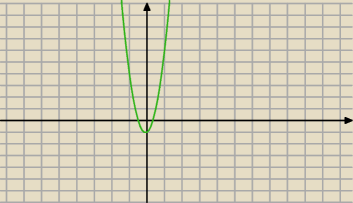
Jerzy: To jest wykres: 6x² + x −1 Dla jakich x przyjmuje wartości ujemne ?

marcin: wewnatrz tej paraboli czyli (−1/2,1/3) ale to juz kompletnie w glowie mam nic jak jest 6x² + x − 1< 0 jak jest mniejsze do 0 to myslalem ze prabaola jest odwrocona ramionami w dol

Jerzy: Parabola ma ramiona zwrócone w dół, gdy współczynnik przy x jest ujemny

marcin: ale jestem debilem jee parabola chyba zalezy od parametru "a" jak jest dodatni to w gore jak ujemny to w dol... chhyba mam jakies przebylski o jezu

marcin: to zmienia postac rzeczy

marcin: Dobra funkcje kwadratowa sobie przypomnialem wow... dzieki

marcin: a chcesz zerknac na macierz 4x4 i zobaczyc czy wynik mi sie zgadza?

marcin: |1 0 2 1| |2 2 4 1| |3 3 8 1| |4 5 2 1| przeksztalcilem to tak ze 1 kolumne przemnozona przez −1 dodalem do 2 kolumny co daje |1 0 2 1| |2 0 4 1| |3 0 8 1| |4 1 2 1| teraz moge wykreslic kolumne 2 i wiersz 4 i mam cos takiego 1*(−1)⁴+2 razy wyznacznik 3na3 |1 2 1| |2 4 1| |3 8 1| =(4+16+6−12−8−4)*1 = 2