ostrosłup ola: Krawędź boczna ostrosłupa prawidłowego czworokątnego ma 12 . Miara kata między krawędziami bocznymi ostrosłupa należącymi do jednej ściany jest równa α. Oblicz pole przekroju tego ostrosłupa płaszczyzną , która przechodzi przez przekątną podstawy i jest prostopadła do krawędzi bocznej ostrosłupa

Maciess: "Oblicz pole przekroju tego ostrosłupa płaszczyzną" ?

ola: Oblicz pole przekroju tego ostrosłupa płaszczyzną− tak tak jest w zadaniu

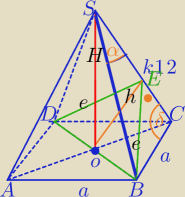
Mila: BE⊥SC 1) W ΔBCS: a²=k²+k²−2k*k*cosα a²=12²+12²−2*12*12 cosα a²=288−288 cosα a²=288(1−cosα) 2)

	180−α
δ=		=90−α/2
	2

	e		e
sinδ=		⇔sin(90−α/2)=
	a		a

e=a*cosα/2

	1
|OB|=		a*√2
	2

h²+|OB|²=e²

	1		1
h2=a2cos2(α/2)−		a2*2=a2cos2(α/2)−		a2
	4		2

	1
h2=a2*(cos2(α/2)−		)
	2

h=a√(cos²(α/2)−¹₂)

	1
3) PΔDBE=		*a√2*h=
	2

	1
=		*a*√2*a√(cos2(α/2)−12)=
	2

	1
=		a2√2 *√(cos2(α/2)−12)=
	2

	1
=		*288(1−cosα)*√2*√(cos2(α/2)−12)=
	2

	√2cos2(α/2)−1
PΔDBE=288*(1−cosα)*√2*
	√2

P_ΔDBE=288(1−cosα)√cosα ============================