funkcja vvool: Dana jest funkcja f(x)=4^|x|+2(2m+1)*2^|x|+4m²−5. Dla jakich wartości m ∊ R nierówność f(x)>0 jest prawdziwa dla wszystkich x∊R?

vvool: up

Jerzy: Podstaw: 2^|x| = t i t > 0. Potem ustal warunki dla trójmianu.

iteRacj@: Zauważ, że 4^|x|=(2^|x|)², możesz podstawić zmienną pomocniczą.

Jerzy: I rozwiązanie: m < 1

vvool: 2⁽|x|)=t>0 v(t)=t²+2(2m+1)*t+4m²−5 współczynnik przy x² jest dodatni plus szukam v(t)>0 czyli najlepiej jakby Δ<0 czy jeszcze jakieś warunki?

Jerzy: To jedyny,ale ja pomyliłem się w rachunkach. Odp: m < −3/2

vvool: odpowiedzią powinno być

	3		−1+√3
m∊(−∞;−		)U(		;+∞)
	2		2

ICSP: Nic nie przeszkodzi jeżeli wielomian będzie miał dwa pierwiastki mniejsze od 1.

Jerzy: Faktycznie, trójmian może mieć rozwiązania, ale nidodatnie ( pierwszy warunek )

Jerzy: Racja, 2^|x| ≥ 1

vvool: czyli 2^x>0 dla każdego x? natomiast 2^|x|≥1 dla każdego x?

Jerzy: Tak.

vvool: ciekawe, pierwszy raz z takim warunkiem się spotykam

Jerzy: Popatrz na wykres funkcji f(x) = 2^x i zauważ,że dla x ≥ 0 , f(x) ≥ 1

vvool: czyli następny warunek Δ=0 ∧ t₀=1

Jerzy: 1) Δ ≥ 0 2) x_w < 1 3) f(1) > 0

Jerzy: Te warunki zapewniają,że pierwiastki trójmianu są mniejsze od 1

vvool: Nie rozumiem warunku 2) x_w<1

Jerzy: x_w to odcięta wierzchołka paraboli.

vvool: No tak tylko czemu ma być mniejsza od 1 a nie od 0 np?

ICSP: Jeżeli masz funkcję kwadratową o dwóch różnych pierwiastkach to jedno z tych rozwiązań jest większe od odciętej wierzchołka a drugie mniejsze. Gdyby wierzchołek byłby większy bądź równy 1 to i jedno rozwiązanie musiałby być większe od 1. Zakładając, że x_w < 1 i f(1) > 0 dostajemy pierwiastek z przedziale (x_w ; 1) − zastanów się z jakiej reguły jest to wniosek. Drugi jak już wcześniej napisałem jest mniejszy od x_w.

vvool: aaaa czaje, że wierzchołek jest pomiędzy miejscami zerowymi na osi X, nie na osi Y

Jerzy: Naszkicuj parabolę o gałęziach do góry i dwóch pierwiastkach mniejszych od 1 i przeanalizuj jeszcze raz te trzy warunki.

Jerzy: Odcięta wierzchołka jest dokładnie w środku między pierwiastkami lub jest pierwiastkiem,gdy Δ = 0

vvool: ten warunek 2) x_w<1 po prostu pomylił mi się z warunkiem dotyczącym f(x_w)<1 chodzi o to, że działamy na argument, a nie na wartość funkcji w danym argumencie jeszcze muszę to przeanalizować parę min

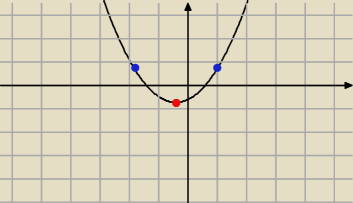
vvool: I czy ta przykładowa parabola spełnia te warunki? Δ>0 bo ma 2 pierwiastki x_w <1 g(1) >0 niebieska kropka czy źle coś?

Jerzy: Tak.Zauważ,że obydwa miejsca zerowe są mniejsze od 1

vvool: To źle czy dobrze?

Jerzy: Dobrze. Przecież tego chcieliśmy jako drugą opcję.

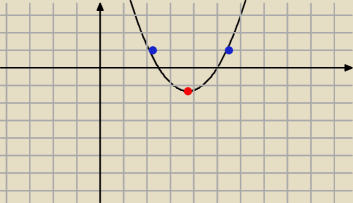
vvool: a co by zmieniło jakby parabola wyglądała w ten sposób? Δ>0 g(1)>0 x_w>1

Jerzy: Obydwa pierwiastki są większe od 1

vvool: mam mętlik w głowie z tym zadaniem bo niby chodzi nam o nierówność f(x)>0 ale funkcja może mieć jednak pierwiastek czegoś nie rozumiem

ICSP: rozwiąż równanie :

	1
2|x| =
	2

vvool: brak rozwiązań

Jerzy: Jeśli t < 1 , to musiałoby być 2^|x| < 1 ,a to jest niemożliwe.

vvool: to czy mój drugi wykres jest zły wobec tego?

vvool: chyba, że chodzi o to, że pasuje pierwszy i drugi i trzeba wyznaczyć skrajny po stronie lewej i pasuje każdy po stronie prawej do nieskończoności?

Jerzy: Kuźwa nudzisz. Ustaliliśmy,że przy Δ ≥ 0 musi być t <1 ,czyli pierwszy wykres.

vvool: dobra możemy tak ustalić i zostawić te zadanie tylko, że ja nie rozumiem skąd te warunki

vvool: powiem więcej mogę od razu dać linka do pełnego rozwiązania tego zadania http://strefamatematyczna.uwm.edu.pl/wamat/zadania/roz_04_04_001_1pg.gif proszę bardzo, ale zadając te zadanie tutaj liczyłem na dojście do tego od początku