odległości,równania,liczby zespolone Jan: Błagam o pomoc w rozwiązaniu tych zadań(lub jakiego kol wiek)! 1. Znajdź takie liczby zespolone (z+1)² = 1+ i 2. Rozłóż na czynniki wielomian w(x)=(x²+2x+1)² +1 3. Znajdź takie liczby zespolone że z²=3+4i 4. Oblicz odległość punktu A(2,5) od okręgu o równaniu x²+ y²+6x−2x+6=0 5. Znajdź równanie stycznej do paraboli o równaniu y²−x=0 przechodzącej przez punkt A(1,1)

Adamm: 2. w(x) = (x+1)⁴+1 = 0

	1+i		1+i
x+1 = ±		, x+1 = ±i
	√2		√2

Mila: 3) z²=3+4i z²=(2+i)²⇔ z=2+i lub z=2−i

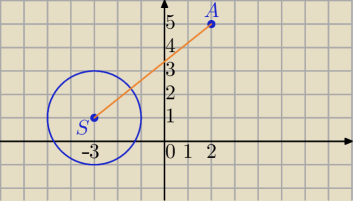
Mila: Oblicz odległość punktu A(2,5) od okręgu o równaniu x²+ y²+6x−2y+6=0 x²+ y²+6x−2y+6=0⇔(x+3)²−9+(y−1)²−1+6=0 (x+3)²+(y−1)²=4 r=2, S=(−3,1) d=|AS|−r d=√5²+4²−2 d=√41−2 [N============]]

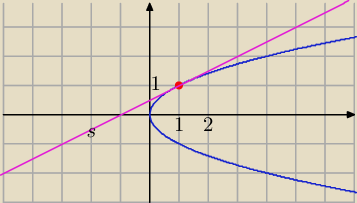
Mila: 5. Znajdź równanie stycznej do paraboli o równaniu y²−x=0 przechodzącej przez punkt A(1,1) F(x,y)=y²−x F_x=−1 F_y=2y Styczna : F₍1)*(x−x₀)+F_y(1)*(y−y₀)=0 ⇔ s: −1*(x−1)+2*(y−1)=0 2y−2=x−1 2y=x+1

	1		1
s: y=		x+
	2		2

=============

Jan: Trochę nie rozumiem skad sie wzielo Fx=−1 i Fy=2y

Mila: 1. Znajdź takie liczby zespolone (z+1)² = 1+ i z+1=√1+i z=−1+√1+i v=√1+i ⇔v²=1+i v=x+iy, x,y∊R (x+iy)²=1+i x²+2xy i−y²=1+i (x²−y²)=1 2xy=1

	1
y=
	2x

	1
x2−		=1 /*4x2
	4x2

4x⁴−1=4x² 4x⁴−4x²−1=0 x²=t, t>0 4t²−4t−1=0 Δ=16+16=32

	4−4√2		4+4√2		1+√2
t=		<0 lub t=		=
	8		8		2

	1+√2
x2=		⇔
	2

	√1+√2		√1+√2
x=		lub x=−
	√2		√2

	2√2		2√2
y=		lub y=−
	1+√2		1+√2

	√1+√2		2√2
z=−1+		+		*i
	√2		1+√2

lub

	√1+√2		2√2
z=−1−		−		*i
	√2		1+√2

============================ Posprawdzaj obliczenia.

PW: Trochę inaczej: (1+i)=(√2(cos(22,5°)+isin(22,5°))², a więc (z+1)²=(√2(cos(22,5°)+isin(22,5°))², skąd z+1=√2(cos(22,5°)+isin(22,5°)) lub z+1=−√2(cos(22,5°)+isin(22,5°)), wystarczy sprawdzić ile wynoszą kosinus i sinus kąta 22,5°.

PW: Korekta: powinno być ⁴√2 zamiast √2.

Mila: Nie miałeś pochodnych funkcji dwóch zmiennych ? Pochodne względem x i względem y F(x,y)=y²−x F_x=−1 zmienną y traktujesz jak stałą F_y=2y, zmienną x traktujesz jak stałą Wzór poprawiam, bo tam stawiłam już współrzędne punktu A=(1,1) A(x₀,y₀)∊wykresu y²−x=0 F_x(x₀)*(x−x₀)+F_y(y₀)*(y−y0)=0