trójkąt mat19: Oblicz długość promienia okręgu opisanego na trójkącie o bokach : 2√5, 2√17, 4√2 i zakoduj trzy pierwsze cyfry rozwinięcia dziesiętnego tego wyniku

6latek:

	a*b*c
R=
	4P

abc dlugosc bokow trojkata P− pole trojkata

mat19: To ja wiem,ale jak obliczyć pole ?

6latek: masz trzy boki to z tw cosinusow liczysz kąt i liczysz pole lub ze wzoru Herona liczysz pole

	a		a
Jesli masz kąt to mozesz tez R obliczyc ze wzoru R=		lub 2R=
	2sinα		sinα

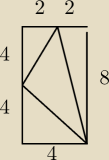
jc: To ten trójkąt w środku. Rysunek może nawet pomóc w znalezieniu promienia.

jc: Pole = 4*8 − 2*4/2 − 2*8/2 − 4*4/2 = 32−4−8−8=12

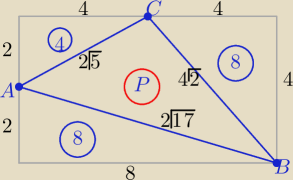Eta: P= P▭ −(8+8+4) = 32−20=12

	2√5*2√17*4√2
R=		=..................
	4*12

Eta:

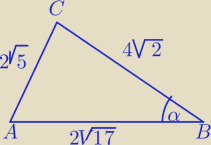
Mila: Z tw. cosinusów (2√5)²=(2√17)²+(4√2)²−2*2√17*4√2 cosα 20=68+32−16√34 cosα

	5
cosα=
	√34

	25		9
sin2α=1−		=
	34		34

	3
sinα=
	√34

2√5
	=2R
sinα

	√34
√5*		=R
	3

	√170
R=
	3

==========

Eta: