funkcja sgn vvool: f(x)=sgn x, podaj wzór funkcji g(x)=f((x−1)(x+3))

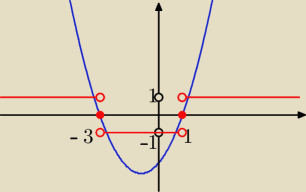
iteRacj@: niebieski wykres h(x)=(x−1)(x+3) czerwony wykres f((x−1)(x+3)), pozostaje tylko zapisać

vvool:

	⎧	−1 gdy x<0
sgn(x)=	⎨	0 gdy x=0
	⎩	1 gdy x>0

coś tu jeszcze nie rozumiem, skoro dla x>0 wartość to 1, to czemu dla

	1
x=		na czerwono jest −1. W końcu ta funkcja jest dla x<0 czy dla f(x)<0 bo
	2

na wykresie czerwony jest −1 gdy f(x)<0 i 1 gdy f(x)>0

signum:

	⎧	−1 dla x∊(−3,1)
sgn(x)=	⎨	0 dla x=−3 v x=1
	⎩	1 dla x∊(−∞,−3)U(1,∞)

vvool: z wykresu wiem ze to powinno tak wygladac tylko mnie dziwi dlaczego tak jest skoro −1 gdy x<0 a napisałeś −1 dla x∊(−3;1) przeciez (0;1) > 0

signum: dla x∊<0,1) g(x)<0 to sgn(x)= −1

vvool: czyli

	⎧	1 gdy f(x)>0
sgn(x)=	⎨	0 gdy f(x)=0
	⎩	−1 gdy f(x)<0

i to by sie zgadzało tutaj natomiast

	⎧	1 gdy x>0
sgn(x)=	⎨	0 gdy x=0
	⎩	−1 gdy x<0

to mi nie pasuje

Eta: kiedy g(x)>0 ano wtedy gdy x∊(−∞,−3)U(1,∞) ( widzisz to na paraboli ? g(x)<0 ⇔ ............... g(x)=0 ⇔ ..............

Jerzy: Czy ty nie widzisz gdzie trójmian przyjmuje wartości dodatnie,a gdzie ujemne ?

Eta: Hej Jerzy

vvool: pewnie ze to widzę to już ma sens tylko bardzo mnie myliło to gdy x<0 to wartość jest −1 i tu się zastanawiałem czy oni podają wartość −1 dla każdego x<0 czy na podstawie wartości −1 podają dopiero x<0 coś takiego: −1 ⇒ x<0 czy x<0 ⇒ −1

vvool: dlatego, że w tej def sgn(x) była mowa o argumentach funkcji a nie wartościach gdzie przyjmuje ujemne

Eta: Nie rób sobie "sieczki" w mózgu

Jerzy: Witaj Eta

vvool:

	⎧	1 gdy x>0
sgn(x)=	⎨	0 gdy x=0
	⎩	−1 gdy x<0

to jakbyście to słownie za interpretowali? bo na Wikipedii nie widzę uzasadnienia dobrego ja to rozumiem tak: wartość funkcji równa się jeden dla każdego x należącego do przedziału obustronnie otwartego od −∞ do 0 wartość funkcji równa się 0 gdy x równa się 0 wartość funkcji równa się −1 dla każdego x należącego do przedziału od 0 do +∞ obustronnie otwartego czy robię błąd?

Eta: g(x)= sgn[(x−1)(x+3)]

	⎧	1 dla x∊(−∞,−3)U(1,∞)
g(x)=	⎨	0 dla x= −3 v x=1
	⎩	−1 dla x∊(−3,1)

taki ma być poprawny zapis funkcji g(x)

vvool: nie zrozumieliście do końca o co mi chodziło, ale ja już zrozumiałem i rozwiałem swoje wątpliwości dzięki za pomoc dla przykładu f(x)=sgn x, oblicz h(x)=f(x−1) lub sgn(x−1)

	⎧	1 dla x∊(1;∞)
h(x)=	⎨	0 dla x=1
	⎩	−1 dla x∊(−∞;1)

Eta: I tak trzymaj