Geometria Analityczna
M:
W równoramiennym trójkącie prostokątnym punkt A=(3,1) jest wierzchołkiem kąta ostrego.
Przeciwległa do niego przyprostokątna zawiera się w prostej o równaniu y=x+1.
Napisz równania prostych zawierających pozostałe boki trójkąta.Już to zrobiłem oznaczając
współrzędne wierzchołka B jako(a,a+1) i korzystając z długości |AB| oraz odległości punktu od
prostej,ale
dlaczego nie wychodzi to z tego,że przyjmujemy,że prosta AB skoro jest to trójkąt prostokątny
równoramienny będzie miała a=tg45=1 czyli y=x+b czyli podstawiając punkt A=(3,1) to y=x−2?
No bo potem przecież żeby odszukać punkt B,to x−2=x−1 ale to nie ma sensu bo to fałsz,coś mi
się wydaję,że chyba jakoś źle patrzę
Janek191:
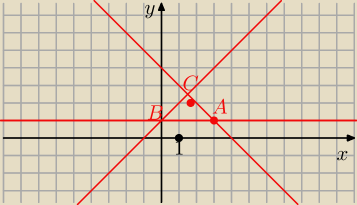
y = x + 1
Prosta prostopadła
y = − x + b przechodzi przez A = ( 3, 1), więc
1 = − 3 + b ⇒ b = 4
zatem
y = − x + 4
oraz
y = 1 − równanie prostej przechodzącej przez przeciwprostokątną ΔABC
 W równoramiennym trójkącie prostokątnym punkt A=(3,1) jest wierzchołkiem kąta ostrego.
Przeciwległa do niego przyprostokątna zawiera się w prostej o równaniu y=x+1.
Napisz równania prostych zawierających pozostałe boki trójkąta.Już to zrobiłem oznaczając
współrzędne wierzchołka B jako(a,a+1) i korzystając z długości |AB| oraz odległości punktu od
prostej,ale
dlaczego nie wychodzi to z tego,że przyjmujemy,że prosta AB skoro jest to trójkąt prostokątny
równoramienny będzie miała a=tg45=1 czyli y=x+b czyli podstawiając punkt A=(3,1) to y=x−2?
No bo potem przecież żeby odszukać punkt B,to x−2=x−1 ale to nie ma sensu bo to fałsz,coś mi
się wydaję,że chyba jakoś źle patrzę
W równoramiennym trójkącie prostokątnym punkt A=(3,1) jest wierzchołkiem kąta ostrego.
Przeciwległa do niego przyprostokątna zawiera się w prostej o równaniu y=x+1.
Napisz równania prostych zawierających pozostałe boki trójkąta.Już to zrobiłem oznaczając
współrzędne wierzchołka B jako(a,a+1) i korzystając z długości |AB| oraz odległości punktu od
prostej,ale
dlaczego nie wychodzi to z tego,że przyjmujemy,że prosta AB skoro jest to trójkąt prostokątny
równoramienny będzie miała a=tg45=1 czyli y=x+b czyli podstawiając punkt A=(3,1) to y=x−2?
No bo potem przecież żeby odszukać punkt B,to x−2=x−1 ale to nie ma sensu bo to fałsz,coś mi
się wydaję,że chyba jakoś źle patrzę
 y = x + 1
Prosta prostopadła
y = − x + b przechodzi przez A = ( 3, 1), więc
1 = − 3 + b ⇒ b = 4
zatem
y = − x + 4
oraz
y = 1 − równanie prostej przechodzącej przez przeciwprostokątną ΔABC
y = x + 1
Prosta prostopadła
y = − x + b przechodzi przez A = ( 3, 1), więc
1 = − 3 + b ⇒ b = 4
zatem
y = − x + 4
oraz
y = 1 − równanie prostej przechodzącej przez przeciwprostokątną ΔABC