odcinek vvool: Dany jest odcinek o końcach A=(1;2), B(−1;−4). Funkcja f przyporządkowuje odciętej dowolnego punktu P należącego do odcinka AB odległość |PR|, gdzie R=(0,1). Wyznacz wzór, zbiór wartości i wartość najmniejszą funkcji f.

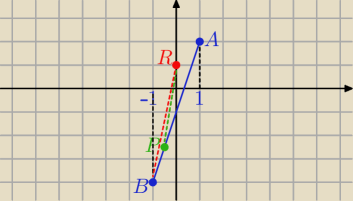
Eta: prosta AB : y=3x−1 to P(x,3x−1) i R(0,1) |PR|=f(x)= .............. = √10x²−12x+4 i x∊<−1,1>

	12
xmin=		=3/5 to f(3/5)=fmin= ....... = √10/5
	20

f_max = f(−1)=...... =√26 ZW= < ........... , .... >

vvool:

	√10
ZW:y∊<		;√26>
	5

	√10
m=
	5

Ciekawe zadanie tak czułem, że trzeba będzie prostą AB wyznaczyć, tylko obawiałem się, że znajdę punkt z poza odcinka. Tyle, że została ta funkcja ograniczona Z tym x_min to trójmian kwadratowy brak mz, funkcja zawsze dodatnia najmniejsza wartość w wierzchołku. Chociaż pierwsze co to liczyłem pochodną złożoną przy czym się trochę pogubiłem zanim dotarłem do wyniku Dzięks za pomoc 👌