optymalizacyjne vvool: Jakie jest największe możliwe pole prostokąta, którego wierzchołki leżą, na bokach trójkąta równobocznego o boku a?

Pytający: 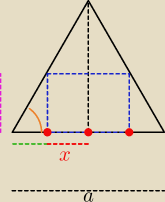x∊(0, a/2) h=(a/2−x)tg(60°)=√3(a/2−x) P(x)=2hx=2√3(a/2−x)x ...

vvool:

	2√3ax
P(x)=		−2√3x2=ax√3−2√3x2
	2

P(x)'=a√3−4√3x

	a
P(x)'=0⇔a√3−4√3x=0 ⇔ x=
	4

a

a

a

a

a

2√3a2

√3a2

P=2√3(

−

)*

=2√3*

*

=

=

2

4

4

4

4

16

8

Pytający: Wygląda ok. Można jeszcze dopisać, że: P'(x)>0 dla x∊(0, a/4) P'(x)<0 dla x∊(a/4, a/2) i dlatego dla x=a/4 jest maksimum.

Eta: Można bez pochodnych .... tylko z funkcji kwadratowej