trójkąt równoboczny nick: Na boku AC trójkąta równobocznego ABC obrano punkt D także |AD|: |DC|=1:2 Oblicz tangens kąta BDC i wyznacz stosunek promieni okręgów wpisanych w trójkąty ABD i BCD

wredulus_pospolitus: A coś od siebie

nick:

wredulus_pospolitus: A przynajmniej rysunek zrobiony został A może (zaszalejemy) wyliczone |BD|

Eta: A ja bez "szaleństwa"

	|BD|
2R1=2R2=
	sin60o

	R1
to		= 1
	R2

≈≈≈≈≈≈≈≈≈≈

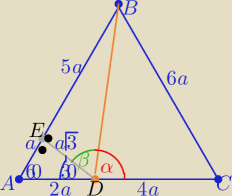
Eta: No i bez wyznaczania długości BD

	5		5√3
tgβ=		=
	√3		3

	tg30o+tgβ
tgα=tg(180o−(30o+β))= − tg(30o+β) =
	tg30o*tgβ−1

	√3   5√3   + 3   3		6√3
tgα =		=		=3√3
	√3   5√3   * −1 3   3		2

tgα= 3√3 ≈≈≈≈≈≈≈≈≈ i po bólu

	tgα+tgβ
korzystałam ze wzoru tg(α+β}=		i z trójkąta "ekierki " 30o,60o,90o
	1−tgα*tgβ

Mila: Okręgi wpisane.

Eta: Ajjj ... przeczytałam opisane

Eta: |BD|=√25a²+3a² = 2√7

	1
P1=P(ABD)=		*6a*2a*sin60o = ...= 3a2√3 , P2= 6a2√3
	2

	6a+2a+2a√7
p1=		= a(4+√7) p2=.....= a(5+√7)
	2

Ze wzoru P=rp ......................... r₁=..... , r₂=......

r1
	= ......
r2

dokończ obliczenia