nie istnieje granica jednostronna analiza: Narysuj funkcję, która spełnia warunek: w x=2 nie istnieje granica lewostronna funkcji, a funkcja jest określona na otoczeniu x=2 Jedyne co znalazłam, to to, że przykład funkcji w której nie istnieją (z resztą obie) granice jednostronne to sin (1/x) w x=0, zatem u mnie by było: sin (1/x−2) w x=2 ale pytanie jak to narysować, bo chyba nie bardzo się da bez kompa/programu i czy rzeczywiście spełnia te warunki? Znacie jakąś inną funkcję, która by spełniała te założenia?

wredulus_pospolitus:

	⎧	1 dla x∊Q\{2}
f(x) =	⎩	0 dla x∉Q

wredulus_pospolitus: powyższa funkcja: 1) nie jest określona w x=2 2) nie posiada granicy lewostronnej (prawostronnej zresztą też, ale tutaj zadanie nie narzuca nam niczego) Warunki zadania spełnione

analiza: Aha... Bo nie musze mieć ciągłości... i mam tylko punkty? i wtedy nie ma granicy?

analiza: Albo nie, nie umiem sobie tego wyobrazić... A tym bardziej narysować

wredulus_pospolitus: jednak łatwiej będzie narysować coś takiego: f(x) = {1 gdy x∊A\{2} &0 gdy x∉A}

	(x+2)−1
gdzie A = {x∊R ;		∊Q}
	2

I będzie to prosta y = 0 z szeregiem punktów 'pustych' dla których funkcja będzie przyjmować

	5
wartość y=1 (począwszy od x = −		'zagęszczając' się coraz bardziej zbliżając się do x=−2
	2

	3
i później symetrycznie będąc coraz rzadziej aż do x = −
	2

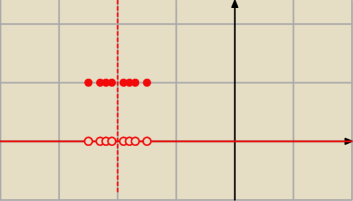
wredulus_pospolitus: tak mniej więcej będzie wyglądała ostatnia zaproponowana funkcja (oczywiście Ty rysując 'dokładniej' możesz pokazać otoczenie x = −2

analiza: Rozumiem, że mówiłes o otoczeniu x=2?

	x−2
I		?
	2