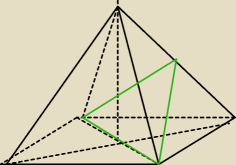
 Podstawą ostrosłupa o równych krawędziach bocznych jest prostokąt, którego boki mają długość 6
cm i 8 cm. Długość wysokości ostrosłupa jest równa 12 cm. Oblicz pole przekroju ostrosłupa
płaszczyzną przechodzącą przez jedną z przekątnych podstawy i równoległą do krawędzi bocznej
ostrosłupa.
We wskazówce mam, że opisany trójkąt jest trójkątem równoramiennym, którego długość wysokości
jest równa połowie krawędzi bocznej ostrosłupa.
Byłby mi ktoś w stanie wytłumaczyć dlaczego lub w jaki sposób inaczej to obliczyć?
Prawidłowa odpowiedź to 32,5 cm2.
Podstawą ostrosłupa o równych krawędziach bocznych jest prostokąt, którego boki mają długość 6
cm i 8 cm. Długość wysokości ostrosłupa jest równa 12 cm. Oblicz pole przekroju ostrosłupa
płaszczyzną przechodzącą przez jedną z przekątnych podstawy i równoległą do krawędzi bocznej
ostrosłupa.
We wskazówce mam, że opisany trójkąt jest trójkątem równoramiennym, którego długość wysokości
jest równa połowie krawędzi bocznej ostrosłupa.
Byłby mi ktoś w stanie wytłumaczyć dlaczego lub w jaki sposób inaczej to obliczyć?
Prawidłowa odpowiedź to 32,5 cm2.
| AO | SE | |||
Z tw. Talesa. | = | =1⇔|SE|=|EC| | ||
| OC | EC |
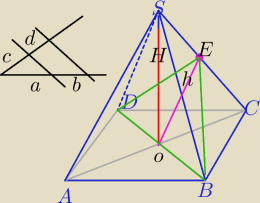 Jeżeli ramiona kąta przetniemy prostymi równoległymi ,
to odcinki wyznaczone na jednym ramieniu są proporcjonalne do odpowiednich odcinków
wyznaczonych na drugim ramieniu.
Jeżeli ramiona kąta przetniemy prostymi równoległymi ,
to odcinki wyznaczone na jednym ramieniu są proporcjonalne do odpowiednich odcinków
wyznaczonych na drugim ramieniu.
| a | c | ||
= | |||
| b | d |
| AO | |
=1 | |
| OC |
| AO | SE | SE | ||||
i | = | ⇔ | =1⇔|SE|=|EC| | |||
| OC | EC | EC |
| 1 | ||
|OE|= | |AS| | |
| 2 |