metodą stycznych newtona fsdaf: Oblicz √2 metodą stycznych newtona.... Wynik to 1,41...oczywiście, ale jaki jest wzór na wyraz następny skoro nie ma x... co mam podstawić po 1.. wyraz piewrszy to 1, a dalej co?

jc: f(x)=x²−2

	1		2
xn+1=		(xn+		)
	2		xn

Wybierz x₀ i licz kolejne wyrazy.

ABC: o gościu od metody trapezów wrócił i znów nie czai... a₀=1 a₁=1/2(1+2/1)=1,5 a₂=1/2(1,5+2/1,5)=1,41(6) a₃=1/2(1,41(6)+2/(1,41(6))=1,41421586... a_n+1=1/2(a_n+2/a_n) i tak to idzie

fsdaf: Dlaczego x² −2? i dlaczego 1/2

ABC: chyba twoja ostatnia sesja się zbliża masz jakiekolwiek pojęcie o metodzie Newtona? rozwiązujesz równanie x²−2=0

fsdaf: No tak, jutro jest, ale tamte całki numeryczne pozdawałem... a teraz mnie w konia robiicie bo wzór jest inny wyraz pierwszy minus wartości funkcji przez pochodną wartości funkcji. Hę.. i dlatego nie wiem skąd wzór... ale podstawiłem do tego powyżej i działą. Ale jutro mam egzamin... troszkę póżno zaczołem... a jak jesteście tacy mili, to tylko powiedzcie mi skąd się wzięło ten wzór x²−2

fsdaf: tak, ja wiem... pan profesor mi wytłumaczył https://www.youtube.com/watch?v=vxI8dp3itMc jak się go puści w 1,25x to się go dobrze słucha. lol...

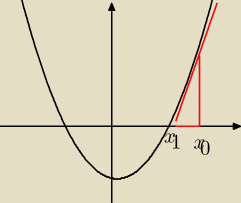
jc: Nachylenie stycznej w punkcie x₀: f'(x₀) = f(x₀)/(x₁−x₀)

	f(x0)
Stąd x1=x0+
	f'(x0)

Weź teraz f(x)=x²−2, a otrzymasz żądany wzór.

fsdaf: albo inaczej, jak do tego dojść... bo rzouymiem że jak się przenieseie na derugą stronę to otrzymamy √2.. natomiast jeszcze mam pytanie, jak to zrobić dla π jego wartość wyliczyć.

fsdaf: pewnie coś z tg trzeba bedzie użyć. albo coś.. ale nie wiem, ja się nie znam... nie jestem matematykiem ;−; xd

ABC: π tak prosto nie da się wyliczyć niestety

ABC: jest szereg potęgowy arcus tangens ale nie sądzę żebyś to przyswoił

fsdaf: wyraz poprzedni minus tangens wyraz poprzedniego. taki jest wzór.. właśnie dostałem excelki..; hmmm mniammm... Panowie.. i wynik rzeczywiście wychodzi poprawny 3,14.... tylko... oczywiście nie wiem dlaczego x−tgx

fsdaf: panowie, a mam pytanie, czy w regula falsi , każde zadanie wygląda tak samo? tylko muszę wybrać odpowiedni przedział, i wartości kolejnych licza się zawsze z tego samego wzoru?

ABC: zależy co nazywasz regula falsi są różne wersje, jedne zakładają przeciwne znaki na krańcach przedziału , inne nie

jc: Niby można: x_n+1 = x_n + sin 2x_n 3.0 3.14112000806 3.14159265357 3.14159265359 3.14159265359

jc: x_n+1 = x_n + sin x_n (bez 2)