Wyznacz pole trójkąta, dla którego bok AB ma najkrótszą długość. Zagubiony: Witam, Mam zadanie "Dany jest trójkąt ABC, w którym bok AC ma długość a oraz kąt ACB ma miarę 45. Wyznacz pole tego trójkąta, dla którego bok AB ma najkrótszą długość. Rozrysowalem wszystko i od 30 minut jestem w jakimś martwym punkcie, nie widzę w jaki sposób oprzeć pola na boku AB. Proszę o pomoc.

wredulus_pospolitus: wzór na pole P_Δ = |AC|*|BC|*sinα z tw. cosinusów: |AB|² = |AC|² + |BC|² − 2|AB||BC|cosα z drugiego wyznaczasz |BC| i podstawiasz co to masz do wzoru na pole ... i już masz pole uzależnione od boku |AB|

wredulus_pospolitus: można też to zrobić o wiele wiele wieleeeeee prościej

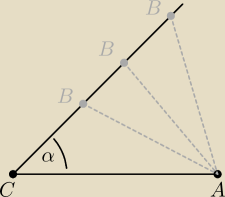
wredulus_pospolitus: |AC| jest stałe ... kąt jest stały ... więc BC jest zawsze pod takim samym kątem względem AC ... gdzie musi się znajdować punkt B (względem punktu A) aby AB było najkrótsze. Innymi słowy −−− masz prostą zawierającą BC i punkt A ... 'najkrótsza' odległość punktu A od prostej zawierającej odcinek BC jest kiedy ? I jak się ją wyznacza (nie chodzi o gotowy wzór)?