OBLICZANIE POLA TRÓJKATA ika: Punkty K,L,M leżą odpowiednio na bokach AB, BC, CA trójkata ABC, Przy czym stosunek AK/KB=BL/LC=CM/MA=1/3 Punkt P leżący wewnątrz trójkąta połączono odcinkami ze wszystkimi wymienionymi punktami. Jaką część pola trójkata ABC stanowi łączne pole trójkątów APK, BPL I CPM?

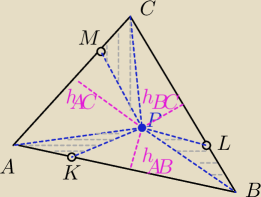
iteRacj@: h_AC, h_BC, h_AB to odpowiednio wysokości trójkątów o wierzchołku P pole całego trójkąta ABC jest sumą pól trzech mniejszych

	1		1		1
PABC=PAPC+PAPB+PBPC=		*|AB|*hAB+		*|BC|*hBC+		*|AC|*hAC
	2		2		2

P − tak oznaczam łączne pole trójkątów ΔAPK, ΔBPL i ΔCPM

	1		1		1
P=		*|AK|*hAB+		*|BL|*hBC+		*|CM|*hAC
	2		2		2

	1
AK:KB=BL:LC=CM:MA=
	3

z tego wynika, że

	1
|AK|=		|AB|
	4

	1
|LB|=		|BC|
	4

	1
|CM|=		|AC|
	4

	1		1		1		1		1		1
P=		*		|AB|*hAB+		*		|BC|*hBC+		*		|AC|*hAC
	2		4		2		4		2		4

	1
wyłączam przed nawias powtarzający się ułamek
	4

	1		1		1		1
P=		(		*|AB|*hAB+		*|BC|*hBC+		*|AC|*hAC)
	4		2		2		2

zauważam, że suma w nawiasie to pole ΔABC obliczone powyżej

	1
P=		*PABC
	4

	1
więc szukane pole to		pola całego trójkąta
	4

ika: Serdeczne dzięki teraz wszystko jasne!

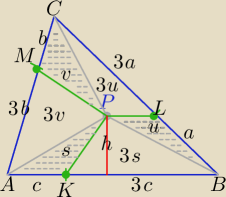Mila: P_ΔABC=P 1) ΔAKP i ΔKBP mają tę samą wysokość h

	1
PΔAKP=		c*h=s
	2

	1		1
PΔKBP=		*3c*h=3*(		c*h)⇔PΔKBP=3*PΔAKP
	2		2

Analogicznie w pozostałych Δ są takie zależności między polami odpowiednich Δ. Zaznaczam na rysunku. 2) Sumujemy pola małych Δ: 4s+4u+4v=P /:4

	1
s+u+v=		P⇔
	4

	1
PΔAPK+PΔ BPL+ PΔ CPM=		PΔABC
	4

=============================