OBLICZANIE POLA CZWOROKATA ika: Środki przeciwległych boków czworokąta wypukłego ABCD połączono odcinkami tworząc cztery czworokąty. Pole "małego" czworokoata zawierającego punkt A ma pole PA,podobnie pole małego czworokata zawierającego punkt B jest równe PB, a pole małego czworokąta zawierąjacego pkt C jest równe PC. Oblicz pole czwartego malego czworokąta

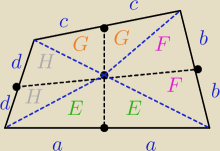
wredulus_pospolitus: zastanów się dlaczego pola trójkątów są równe (zaznaczone literami oznaczają, które pola są równe)

wredulus_pospolitus: i wykorzystaj to do wyznaczenia P_D = H + G

ika: No tak ale tu nie ma żadnych danych więc jak obliczyć Pd?

ika: 1/2 polaA +1/2 pola C?

wredulus_pospolitus: Bzdura zauważ, że: P_D = H+G = (H+E) − (E+F) + (F+G) = P_A − P_B + P_C

teclado: Mam pytanie, bo nie rozumiem jak H+G=(H+E)−(E+F)+(F+G) Jaka jest to zależność?

kinia:

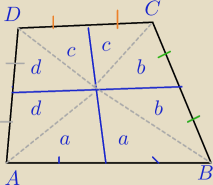
Mila: (*) P_A=a+d (**) P_B=a+b (***) P_C=b+c P_D={C[c+d=?]] P_C+P_A=a+b+c+d sumuję pola dwóch czworokątów w których mamy pola c i d P_B=a+b ===========(−) P_A+P_C−P_B=c+d