ekstrema funkcji vvool: Jak wyznaczyć ekstrema funkcji f(x)=|x²−1|?

Jerzy: Naszkicować. Dwa minima lokalne 0 i jedno maksimum 1

vvool: Czy można to zrobić algebraicznie czy wyłącznie rysunkiem? Bo zależy mi na algebraicznym.

Jerzy: Można, ale analizujesz tą w oddzielnych przedziałach.

vvool: x²−1 dla x²−1>0 i 1−x² dla x²−1<0?

Jerzy: Tak, w pierwszym przypadku ≥ 0

vvool: f(x)=|x²−1| dla x²−1≥0 ⇒ (x−1)(x+1)≥0 ⇒ x∊(−∞;−1]U[1;∞] f₁(x)=x²−1, f₁(x)'=2x pochodna zmienia znak w x=0 rosnąca czyli to jest min lok dla x²−1<0 ⇒ (x−1)(x+1)<0 ⇒ x∊(−1;1) f₂(x)=1−x², f₂(x)'=−2x pochodna zmienia znak w x=0 czyli to max lok? W pierwszym x=0 ∉(−∞;−1]U[1;∞] W drugim x=0∊(−1;1) I coś źle jest

kochanus_niepospolitus: nie jest źle po prostu dwa ekstrema lokalne są w punktach w których nieistnieje pochodna czyli w x=−1 oraz x=1 (tam gdzie 'zmienia się znak w module' )

kochanus_niepospolitus: co łatwo się zauważa właśnie poprzez szkic wykresu funkcji

vvool: czyli jak nie istnieje pochodna to nie oblicze ekstremów algebraicznie i tylko pozostaje mi rysunek?

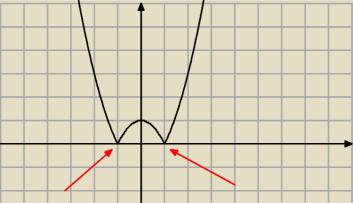
kochanus_niepospolitus: zauważ że w tych dwóch punktach pochodna nieistnieje tak samo jak w f(x) = |x| także za pomocą pochodnej nie wyjdzie Ci żadne ekstremum. Po prostu ono występuje tam gdzie nie można policzyć pochodnej

vvool: no właśnie czemu w f(x)=|x| nie będzie można policzyć pochodnej?

kochanus_niepospolitus: policzysz ekstremum ... wystarczy wykazać,że: ∀_p>r>0 f(x₀) < f(x_o ± r) jest prawdą dla x₀ = −1 oraz x₀ = 1 gdzie 'p' to takie ograniczenie aby nie brać zbyt dużego przedziału (bo wtedy byśmy wybrali x₀ = −1 oraz r=2 i nie prawdą by było, że f(−1) = 0 < 0 = f(1))

Jerzy: Bo lewo i prawo stronne granice ilorazu różnicowego są różne w tym punkcie.

Jerzy: To do pytania z 13:22

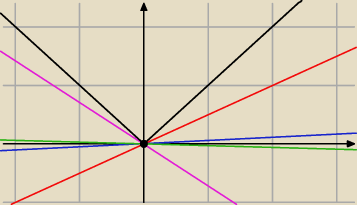
kochanus_niepospolitus: A czym jest wartość pochodnej (w punkcie) Wartość pochodnej w punkcie jest równa współczynnikowi kierunkowemu (a = tgα) STYCZNEJ do tejże funkcji w tymże właśnie punktu. A dla f(x) = |x| w punkcie x₀ = 0 możemy narysować nieskończenie wiele stycznych. Każda z tych kolorowych prostych jest STYCZNA do f(x) = |x| w punkcie x₀ = 0, więc której z nich współczynnik kierunkowy powinno się wybrać? I dlaczego akurat tej a nie innej?

kochanus_niepospolitus: a ogólnie (mało matematycznie) −−− gdy widzisz wykres funkcji i jest tam 'ostre zagięcie' (jak właśnie np. w f(x) = |x²−1|) to właśnie w punktach gdzie masz to 'ostre zagięcie' nie będzie można policzyć pochodnej.

Jerzy: No....dowód to to nie jest,ale obrazowe wytłumaczenie

vvool: Nieźle, świetnie to pokazałeś. W szkole zazwyczaj się liczy te pochodne bez większego zastanowienia jest wzorek i tyle i potem wychodzą takie luki które nie powinny się zdarzyć

vvool: "Jerzy: Bo lewo i prawo stronne granice ilorazu różnicowego są różne w tym punkcie." Tą odpowiedzią jestem również zaciekawiony. Jak należy podejść do tego problemu?

kochanus_niepospolitus: A jak oblicza się pochodną w punkcie Z DEFINICJI

	f(x0+h) − f(x0)
limh−>0
	h

teraz jak masz f(x) = |x| i liczysz w x₀ = 0 to liczysz granicę lewo i prawostronną (wstawiając odpowiednio f(x) = −x dla lewostronnej i f(x) = x dla prawostronnej) I wyjdą Ci różne wartości pochodnej w tymże punkcie.

vvool: h czym jest w tym wzorze ograniczeniem z dwóch stron?

kochanus_niepospolitus: Dodatkowo zauważ, że wartości które otrzymasz tutaj podaje 'zakres' w jakim może się znaleźć współczynnik kierunkowy prostej, aby ona była styczna do f(x) = |x| w punkcie x₀ = 0 Tutaj wyjdzie a ∊ <−1 ; 1> i tylko dla takiego zakresy współczynnika kierunkowego funkcja g(x) = a*x będzie styczna

kochanus_niepospolitus: Jako że liczysz granicę dla h−>0 to nie zajmujesz się ograniczeniem samego 'h' ... po prostu liczysz granicę Szczerze mówiąc ... aby to dobrze Ci wyjaśnić (czym jest 'h' i dlaczego tak a nie inaczej wygląda definicja) potrzebowałbym tablicy (to akurat mógłbym tutaj narysować) i czasu, którego niestety teraz nie mam bo muszę uciekać

vvool: f(x)=|x| w x₀=0 f(0)=0 f(0+h) f(0)'=lim_h−>0^f(h)−f(0)_h=lim_h−>0^|h|_h

vvool: coś takiego?

vvool: nie ma sprawy, to nie jest coś pilnego w tym momencie bo mam ferie i ćwiczę do maturki jak znajdziesz czas to odpisz chętnie się dowiem czegoś nowego