Macierz
jadeit:
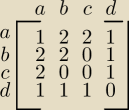
Dana jest macierz sąsiedztw grafu nieskierowanego.
Proszę przeprowadzić obliczenia − korzystając z iloczynu macierzy, ile jest
dróg o długości 3 krawędzi pomiędzy wierzchołkami c i d i wypisać
te wszystkie trasy.
Rozumiem ogólną zasadę mnożenia macierzy, umiem narysować ten graf z macierzy sąsiedztw,
jednak zupełnie nie mam pomysłu jak policzyć te drogi. Ktoś może pomóc?
25 sty 22:27
iteRacj@:
Czy liczbę dróg o długości 3 z wierzchołka C do wierzchołka D należy odczytać z A3, gdzie A
to podana macierzy sąsiedztw grafu?
26 sty 11:21
Pytający:
Tak jak napisałaś Iteracjo. Element aij z macierzy An oznacza liczbę dróg (takich, że
wierzchołki i krawędzie mogą się powtarzać) długości n z wierzchołka i do wierzchołka j.
A =
1 2 2 1
2 2 0 1
2 0 0 1
1 1 1 0
A2 =
10 7 3 5
7 9 5 4
3 5 5 2
5 4 2 3
A3 =
35 39 25 20
39 36 18 21
25 18 8 13
20 21 13 11
Graf jest nieskierowany, więc macierze są symetryczne.
Niżej przez (xy)n rozumiem drogę długości n z x do y.
13 (cd)3 =
=
3*1 (ca)2d + // (ca)2, czyli trzeci wiersz A razy pierwsza kolumna A
5*1 (cb)2d + // (cb)2, czyli trzeci wiersz A razy druga kolumna A
5*1 (cc)2d = // (cc)2, czyli trzeci wiersz A razy trzecia kolumna A
=
2 caad +
1 cdad +
+
2*2 cabd +
1 cdbd +
+
2*2 cacd +
1 cdcd
26 sty 15:58
iteRacj@: bardzo przejrzyście wyjaśnione, dzięki!
26 sty 16:32
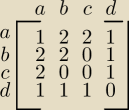 Dana jest macierz sąsiedztw grafu nieskierowanego.
Proszę przeprowadzić obliczenia − korzystając z iloczynu macierzy, ile jest
dróg o długości 3 krawędzi pomiędzy wierzchołkami c i d i wypisać
te wszystkie trasy.
Rozumiem ogólną zasadę mnożenia macierzy, umiem narysować ten graf z macierzy sąsiedztw,
jednak zupełnie nie mam pomysłu jak policzyć te drogi. Ktoś może pomóc?
Dana jest macierz sąsiedztw grafu nieskierowanego.
Proszę przeprowadzić obliczenia − korzystając z iloczynu macierzy, ile jest
dróg o długości 3 krawędzi pomiędzy wierzchołkami c i d i wypisać
te wszystkie trasy.
Rozumiem ogólną zasadę mnożenia macierzy, umiem narysować ten graf z macierzy sąsiedztw,
jednak zupełnie nie mam pomysłu jak policzyć te drogi. Ktoś może pomóc?