dowód, geometria xxx: W trójkącie ABC punkty D,E leżą odpowiednio na bokach AB i AC tak, że |AD|DB|=1:2 oraz |AE|EC|=2:1. Wyznacz jaką część pola trójkąta ABC stanowi pole czworokąta ADFE. (proszę bez linków do innych stron, to co jest dostępne w internecie już widziałam i wciąż nie rozumiem, także będę bardzo wdzięczna za pomoc)

xxx: ...

Eta:

	2
P(ADFE)=		P(ABC)
	7

xxx: Dziękuję, tylko skąd się to bierze?

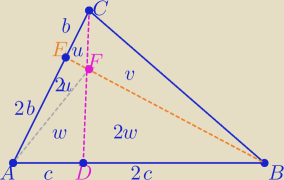Eta: Dla trójkątów ADC i DBC : 2(3u+w)=v+2w ⇒ v= 6u dla trójkątów ABE i BCE : 2(u+v)=2u+3w⇒ 14u=2u+3w ⇒ w=4u P(ABC)= 3u+3w+v= 21u P(ADFE)= 2u+w = 6u

P(ADFE)		6u		2
	=		=
P(ABC)		21u		7

	2
P(ADFE)=		P(ABC)
	7

==================

xxx: Bardzo dziękuję!

Eta: Czy wszystko jasne ?

Mila:

	1
1) PΔ=		a*h
	2

P_ΔABC=P a=3x, b=3y

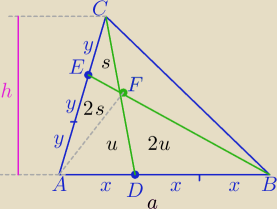
	1		1		1
2) PADC=		*(		a*h)=		P
	2		3		3

analogicznie :

	2
PΔCDB=		P
	3

	2
PAEB=		P
	3

3) Rozważamy jakie są zależności pól w małych Δ ΔADF i ΔDBF mają taką samą wysokość P_ΔDBF=2*P_ΔADF zaznaczyłam pola na rysunku: 2u, u ΔCEF i ΔEFA mają taką samą wysokość, pola zaznaczone na rysunku: s, 2s 4)

	1
s+2s+u=		P
	3

	2
2s+u+2u=		P
	3

−−−−−−−−−−

	1
3s+u=		P *(−3)
	3

	2
2s+3u=		P
	3

=========== −9s−3u=−P

	2
2s+3u=		P
	3

==========

	1		4
s=		P, u=		P
	21		21

5)

	1		4		6
PADFE=2*		P+		P=		P
	21		21		21

	2
PADFE=		P
	7

================

xxx: Tak, tak, dziękuję bardzo jeszcze raz !

Eta: