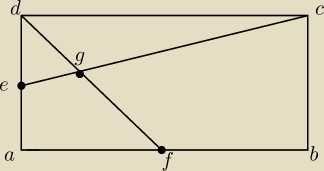
udowodnij że pola są równe arikarik: Punkty E i F są środkami boków prostokąta ABCD. Wykaż, że pole trójkąta DGC jest równe polu czworokąta AEGF.

ICSP: PΔDGC = PΔDEC − PΔEDG P▱AEGF = PΔAFD − PΔEDG stąd wniosek, że PΔDGC − P▱AEGF = PΔDEC − PΔAFD a ponieważ

	1
PΔDEC − PΔAFD =		a * b gdzie a i b są bokami prostokąta
	4

więc PΔDEC − PΔAFD = 0 co daje PΔDGC = P▱AEGF

PW: Wskazówka: Trójkąty CDE i AFD mają równe pola.

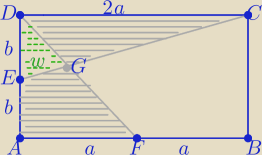
Eta: P(AFD)=ab i P(EDC)=ab P(DGC)=ab−w i P(AEGF)=ab−w wniosek : P(DGC)=P(AEGF) c.n.w. i po bólu