Oblicz objętość bryły obrotowej, powstałej przez obrót wokół osi OX i OY obszaru
MarianoItaliano: Oblicz objętość bryły obrotowej, powstałej przez obrót wokół osi OX i OY obszaru ograniczonego
wykresem funkcji f i osią OX, jeśli:
a) f(x) = x dla x ∊ [0,1]
25 sty 02:27
Jerzy:
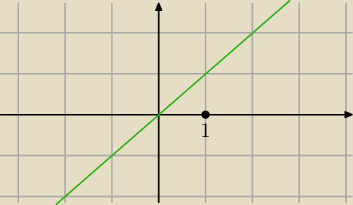
| | 1 | | 1 | | 1 | | 1 | |
Vx = π0∫1x2dx = π[ |
| x3]01 = π[ |
| *1 − |
| *0] = |
| π |
| | 3 | | 3 | | 3 | | 3 | |
wokół osi OY jest to samo wobec symetrii.
| | 2 | |
Ostatecznie: V = 2*Vx = |
| π |
| | 3 | |
25 sty 09:26
lordwajdder: a tam nie powinno być, że to jest pi [ 1/2x2] bo f(x)=x ? czyli ∫ x = ∫1/2x2 ?
25 sty 18:44
Jerzy:
V =π
a∫
bf
2(x)dx
| | 1 | |
f(x) = x , czyli mamy: ∫x2dx = |
| x3 |
| | 3 | |
25 sty 18:46
