Geometria na płaszczyźnie the foxi: Punkty A, B, C dzielą okrąg na trzy łuki, których stosunek długości wynosi 6:8:10. Oblicz cosinus najmniejszego kąta trójkąta, którego wierzchołkami są punkty A, B i C. Proszę o wskazówkę.

ABC: najmniejszy kąt naprzeciwko najkrótszego boku, opartego na najkrótszym łuku 360/(6+8+10)=15 6*15=90 twierdzenie o kątach z których jeden jest dwa razy większy od drugiego

the foxi: dziękuję bardzo, teraz widzę, że zadanie prostsze niż ktokolwiek by pomyślał. wczoraj na maturze próbnej bez skutku kombinowałem nad tym dobre 20 minut

ABC: co do matury: first rule: don't panic!

the foxi: oczywiście, wystarczy wziąć się za "koszmarną" geometrię

Maciess: the foxi ty nie jestes już po maturze?

the foxi: jeszcze nie, dopiero w tym roku

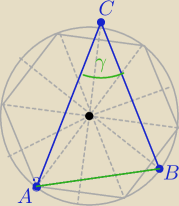
Mila: Mogłeś zrobić rysunek , na pewno by pomogło. 6:8:10=3:4:5 3+4+5=12 Liczymy miarę kąta wpisanego ACB:

3
	*180=45
12

	√2
cos 45o=
	2