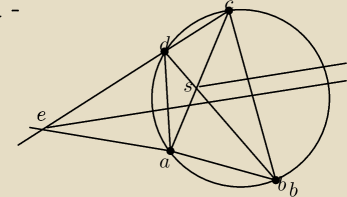
Okrąg opisany na czworokącie i wpisany , zadania na dowodzenie Luki123xx1: W czworokącie ABCD wpisanym w okrąg przedłużono boki AB i CD aż do przecięcia w punkcie E.Przekątne AC i BD przecinają się w Punkcie S.Wskaż że dwusieczna kąta BEC jest równoległa do dwusiecznej kąta BSC.Przy S jest kąt oraz przy E jest kąt który dzieli na dwa takie same kąty . Z góry dziękuję

LUKI332: Proszę o pomoc. Strasznie ważne!

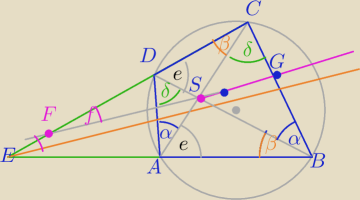
Mila: 1) ∡ABD=∡ACD =β − jako kąty wpisane oparte na tym samym łuku (cięciwa AD) ∡ADB=∡ACB =δ − jako kąty wpisane oparte na tym samym łuku (cięciwa AB) Kąty przeciwległe czworokąta mają w sumie po 180^o. Analogicznie równe pozostałe zaznaczone 2) W ΔBCE: ∡E=180−(α+2β+δ)

1		180−(α+2β+δ)
	∡E=
2		2

==================

	1		180−(α+δ)
3)		∡BSC=
	2		2

Spróbuj dokończyć, nie mogę dzisiaj dłużej byc na forum. Ewentualnie w razie potrzeby jutro

LUKI332: Proszę o dokończenie całości to dla mnie bardzo ważne

LUKI332: Helppp

Mila:

	1
∡CSG=		∡BSC i jest kątem zewnętrznym ΔFCS⇔
	2

180−(α+δ)
	=∡f+β⇔
2

	180−(α+δ)		180−(α+δ)−2β		180−(α+2β+δ)		1
∡f=		−β=		=		=		∡E
	2		2		2		2

⇔proste zawierająca dwusieczną kąta BEC jest równoległa do dwusiecznej kąta BSC.

ite: chyba już po terminie oddania prac...

Mila: Nie wiedziałam , że to jakiś konkurs. Dokończenie nie było trudne.

Mila: Ite, masz inny sposób?

iteRacj@: Pomyślałam o terminie oddania prac zaliczeniowych, semestr się kończy, oceny wystawiają. Wrzutka na wieczór, niech się zadanie przez noc zrobi. A tu dokończyć trzeba!

Mila: I wcale tu nie zagląda