porządek produktowy esteban: Rozważamy zbiór ℛ² z porządkiem produktowym. Niech A={(x,y): x²+y²=1} wskazać kresy i elementy wyróżnione A 1)Czy dobrze myślę że dla porządku produktowego rozważamy tylko II i IV ćwiartkę układu współrzędnych ? 2)Elementy maksymalne : (0,1) ; (1,0) elementy minimalne : (−1,0) ; (0,−1) największy i najmniejszy − czy istnieją? kresy? proszę o pomoc

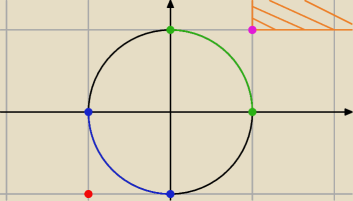
Pytający: 1) Nie, rozważamy cały zbiór A. 2) Źle (a przynajmniej za mało). Elementy maksymalne w A ze względu na porządek produktowy ≤_p to takie a∊A, że nie istnieje b∊A takie, że a ≤_p b. Elementy minimalne analogicznie. Elementy największy i najmniejszy nie istnieją (jeśliby istniały, to byłyby jednocześnie jedynym elementem maksymalnym/minimalnym; poza tym w zbiorze A nie ma nawet jednego elementu porównywalnego ze względu na ≤_p ze wszystkimi elementami z A, więc nie ma mowy o tym, że istnieje większy/mniejszy od wszystkich) Kresów szukasz w ℛ²: ograniczenia górne (c∊ℛ² takie, że dla każdego a∊A zachodzi a ≤_p c), kres górny (najmniejsze z ograniczeń górnych), kres dolny (największe z ograniczeń dolnych).

esteban: Okej , chyba zaczynam rozumieć . łuk jest zbiorem elementów maksymalnych , dlatego że punkty leżące na tym łuku nie są ze sobą porównywalne (i oczywiście spełniają warunek na bycie maksymalnym) ? ja założyłem wcześniej że skoro nie są porównywalne to tego nie rozpatrujemy / Kresy rozumiem już ,ma to sens

iteRacj@: Czy oba czarne łuki razem z końcami należącymi do osi są łańcuchami?

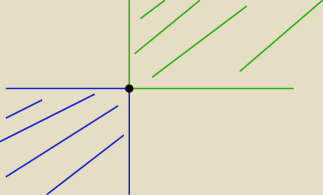
Pytający: Tak łopatologicznie jak weźmiesz dowolny punkt a∊ℛ² to jest on mniejszy (w sensie ≤_p) od każdego punktu z ćwiartki "na prawo i do góry" (wyznaczonej przez tenże punkt) i każdy punkt z ćwiartki "na lewo i do dołu" jest mniejszy (w sensie ≤_p) od tego punktu a. Dla punktów na zaznaczonych łukach w odpowiedniej "ćwiartce" nie ma żadnego punktu należącego do A (różnego od rozpatrywanego punktu), znaczy nie ma elementów (punktów) większych/mniejszych w zbiorze A. A jeszcze odpowiadając konkretnie na pytanie: "łuk jest zbiorem elementów maksymalnych , dlatego że punkty leżące na tym łuku nie są ze sobą porównywalne (i oczywiście spełniają warunek na bycie maksymalnym) ?" Nie. Ten łuk jest zbiorem elementów maksymalnych, bo każdy jego punkt spełnia warunek na bycie elementem maksymalnym. I tylko dlatego. To, że nie są ze sobą porównywalne wynika z tego, że są maksymalne (jeśli jakieś dwa byłyby porównywalne, to któryś musiałby być mniejszy (≤_p) od drugiego i tym samym nie byłby maksymalnym), ale nie na odwrót.

Pytający: Tak Iteracjo, są łańcuchami (w sensie każdy ze wspomnianych przez Ciebie łuków z osobna).

iteRacj@: dzięki !

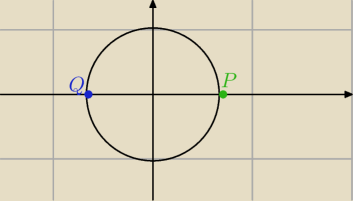
esteban: Czyli w przypadku porządku leksykograficznego ≤_L P jest jednocześnie kresem górnym, elementem maksymalnym i elementem największym, a Q jest kresem dolnym, elementem minimalnym i elementem największym , dobrze myślę ?

Pytający: