wyprowadzenie wzoru w okręgu wpisanym w trójkąt równoramienny rrroback: Dzień dobry. Mam pytanie odnośnie wzoru dotyczącego okręgu wpisanego w trójkąt równoramienny. Nie wiem jak on został wyprowadzony. Dane: trójkąt równoramienny o podstawie a, bokach b i wysokości h. Wpisany okrąg o promieniu r. Wzór: r/0.5a=h−r/b

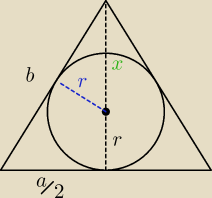
wredulus_pospolitus: x = h−r z podobieństwa trójkątów wynika:

r		x
	=
a/2		b

rrroback: dzięki za odpowiedź, chociaż rozumiem i nie rozumiem. podejrzewałem, że chodzi o podobieństwo trójkątów, ale nie potrafię zobaczyć których

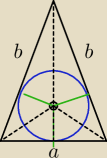
ite: można do udowodnić ze wzorów na pola Δ

	ah
P=
	2

	(a+b+b)r
P=
	2

(a+b+b)r=ah ar+2br=ah a(h−r)=2br (a/2)(h−r)=br

h−r		r
	=
b		a/2

rrroback: dzięki! to zrozumiałem ale chciałbym też zrozumieć opcję z podobieństwem

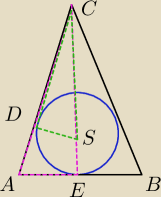
ite: znacznie krócej sposobem Blee ΔACE≈ΔCSD (kkk)

|DS|		|CS|
	=
|AE|		|AC|

r		h−r
	=
a/2		b

Jerzy: Porównujecie stosunek dwóch przyprostokatnych, do stosunku dwóch przciwprostokątnych. Na jakiej podstawie ?

Jerzy: Dlaczego mieszacie do tego trójkąt ASE ?

ite: Z podobieństwa trójkątów w wynika, że najkrótszy bok mniejszego trójkąta do najkrótszego boku większego trójkąta ma się tak, jak najdłuższy do najdłuższego. To się nie zgadza?

ite: ΔASE nie biorę pod uwagę, AE to u mnie najkrótszy bok ΔACE

Jerzy: Tak, teraz się zgadza

ite: uff!

rrroback: Jeszcze raz dzięki Wszystko jasne