Granistosłup
Kingaa:
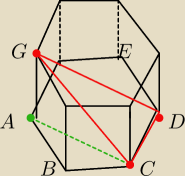
Wszystkie krawędzie graniastosłupa prawidłowego sześciokątnego ABCDEFGHIJKL mają długość a. Z
wierzchołka G poprowadzono przekątne GC oraz GD, które z krawędzią podstawy tworzą przekrój w
kształcie trójkąta. Oblicz pole tego przekroju.
Liczę |AC|= a
√3
Obliczam przekątną CG z Δ ACG |CG|=2a
I w rozwiązaniu mam, że Δ GCD jest prostokątny o kącie prostym GCD, moje pytanie skąd wniosek,
że jest to trójkąt prostokątny?
Mila:
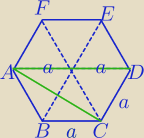
1)
|AC|=a
√3
|AD|=2a
2) W GAC:
|GC|
2=(a
√3)
2+a
2|GC|=2a
3)
W ΔGAD:
|GD|
2=(2a)
2+a
2=5a
2
|GD|=a
√5
4) W ΔGCD:
a, 2a,
√5 a − długości boków
Ztw. Odwrotnego do tw. Pitagorasa:
(
√5 *a)
2=? a
2+(2a)
2
5a
2=5a
2⇔ΔGDC jest prostokątny
Kąt leżący naprzeciw najdłuższego boku jest kątem prostym
 Wszystkie krawędzie graniastosłupa prawidłowego sześciokątnego ABCDEFGHIJKL mają długość a. Z
wierzchołka G poprowadzono przekątne GC oraz GD, które z krawędzią podstawy tworzą przekrój w
kształcie trójkąta. Oblicz pole tego przekroju.
Liczę |AC|= a√3
Obliczam przekątną CG z Δ ACG |CG|=2a
I w rozwiązaniu mam, że Δ GCD jest prostokątny o kącie prostym GCD, moje pytanie skąd wniosek,
że jest to trójkąt prostokątny?
Wszystkie krawędzie graniastosłupa prawidłowego sześciokątnego ABCDEFGHIJKL mają długość a. Z
wierzchołka G poprowadzono przekątne GC oraz GD, które z krawędzią podstawy tworzą przekrój w
kształcie trójkąta. Oblicz pole tego przekroju.
Liczę |AC|= a√3
Obliczam przekątną CG z Δ ACG |CG|=2a
I w rozwiązaniu mam, że Δ GCD jest prostokątny o kącie prostym GCD, moje pytanie skąd wniosek,
że jest to trójkąt prostokątny?
 1)
|AC|=a√3
|AD|=2a
2) W GAC:
|GC|2=(a√3)2+a2|GC|=2a
3)
W ΔGAD:
|GD|2=(2a)2+a2=5a2
|GD|=a√5
4) W ΔGCD:
a, 2a,√5 a − długości boków
Ztw. Odwrotnego do tw. Pitagorasa:
(√5 *a)2=? a2+(2a)2
5a2=5a2⇔ΔGDC jest prostokątny
Kąt leżący naprzeciw najdłuższego boku jest kątem prostym
1)
|AC|=a√3
|AD|=2a
2) W GAC:
|GC|2=(a√3)2+a2|GC|=2a
3)
W ΔGAD:
|GD|2=(2a)2+a2=5a2
|GD|=a√5
4) W ΔGCD:
a, 2a,√5 a − długości boków
Ztw. Odwrotnego do tw. Pitagorasa:
(√5 *a)2=? a2+(2a)2
5a2=5a2⇔ΔGDC jest prostokątny
Kąt leżący naprzeciw najdłuższego boku jest kątem prostym
